设f（x）是定义在R上的偶函数，切f（x）在[0，+∞）上为增函数，则f（-2）、f（-π）、f（3）的大小关系是（ ）
| A．f（-π）>f（-2）>f（3） | B．f（-π）>f（3）>f（-2） |
| C．f（-π）<f（3）<f（-2） | D．f（-π）<f（-2）<f（3） |
已知x2+4y2+kz2=36，且x+y+z的最大值为7，则正数k等于（）
| A．1 | B．4 | C．8 | D．9 |
已知a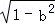
+b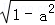
=1，则以下成立的是（）
| A．a2+b2＞1 | B．a2+b2=1 | C．a2+b2＜1 | D．a2b2=1 |
二维形式的柯西不等式可用（）表示．
| A．a2+b2≥2ab（a，b∈R） |
| B．（a2+b2）（c2+d2）≥（ab+cd）2（a，b，c，d∈R） |
| C．（a2+b2）（c2+d2）≥（ac+bd）2（a，b，c，d∈R） |
| D．（a2+b2）（c2+d2）≤（ac+bd）2（a，b，c，d∈R） |
已知a，b∈R，a2+b2=4，求3a+2b的取值范围为（）
| A．3a+2b≤4 | B．3a+2b≤ |
C．3a+2b≥4 | D．不确定 |
设x、y、z是正数，且x2+4y2+9z2=4，2x+4y+3z=6，则x+y+z等于（）
A． |
B． |
C． |
D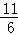． |