设函数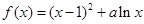 ,
, .
.
(1)若曲线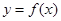 在点
在点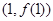 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值;
(2)求函数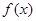 的单调区间;
的单调区间;
(3)若函数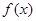 有两个极值点
有两个极值点 ,
,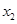 ,且
,且 ,求证:
,求证: .
.
已知 ,函数 .
(1)当 时,解不等式 ;
(2)若关于 的方程 的解集中恰好有一个元素,求 的取值范围.
(3)设 ,若对任意 , ,函数 在区间 , 上的最大值与最小值的差不超过1,求 的取值范围.
双曲线 的左、右焦点分别为 , ,直线 过 且与双曲线交于 , 两点.
(1)直线 的倾斜角为 ,△ 是等边三角形,求双曲线的渐近线方程;
(2)设 ,若 的斜率存在,且 ,求 的斜率.
有一块正方形 , 所在直线是一条小河,收获的蔬菜可送到 点或河边运走.于是,菜地分别为两个区域 和 ,其中 中的蔬菜运到河边较近, 中的蔬菜运到 点较近,而菜地内 和 的分界线 上的点到河边与到 点的距离相等,现建立平面直角坐标系,其中原点 为 的中点,点 的坐标为 ,如图
(1)求菜地内的分界线 的方程;
(2)菜农从蔬菜运量估计出 面积是 面积的两倍,由此得到 面积的经验值为 .设 是 上纵坐标为1的点,请计算以 为一边,另一边过点 的矩形的面积,及五边形 的面积,并判断哪一个更接近于 面积的“经验值”.

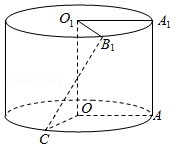
将边长为1的正方形 (及其内部)绕 旋转一周形成圆柱,如图, 长为 , 长为 ,其中 与 在平面 的同侧.
(1)求三棱锥 的体积;
(2)求异面直线 与 所成的角的大小.
已知函数 .
(1)当 时,求不等式 的解集;
(2)设函数 ,当 时, ,求 的取值范围.