选修4—4:坐标系与参数方程选讲.
已知直线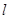 的参数方程为
的参数方程为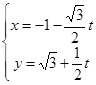 (
(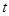 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,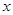 轴的正半轴为极轴建立极
轴的正半轴为极轴建立极
坐标系,圆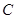 的极坐标方程为
的极坐标方程为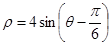 .
.
(1)求圆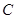 的直角坐标方程;
的直角坐标方程;
(2)若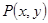 是直线
是直线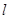 与圆面
与圆面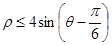 的公共点,求
的公共点,求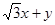 的取值范围.
的取值范围.
(本小题满分13分)
某初级中学共有学生2000名,各年级男、女生人数如下表:
| 初一年级 |
初二年级 |
初三年级 |
|
| 女生 |
373 |
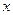 |
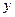 |
| 男生 |
377 |
370 |
 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求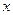 的值;
的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3)已知 ,
, ,求初三年级中女生比男生多的概率.
,求初三年级中女生比男生多的概率.
(本小题满分13分)
已知函数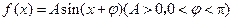 ,
,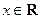 的最大值是1,其图像经过点
的最大值是1,其图像经过点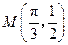 .
.
(1)求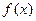 的解析式;
的解析式;
(2)已知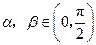 ,且
,且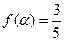 ,
,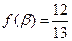 ,求
,求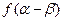 的值.
的值.
已知
的角
所对的边分别是
,设向量
.
(1)若
,求证:
为等腰三角形;
(2)若
,边长
,角
,求
的面积.
已知
是公差为
的等差数列,
是公比为
的等比数列.
(1)若
,是否存在
,有
说明理由;
(2)找出所有数列
和
,使对一切
,
,并说明理由;
(3)若
试确定所有的
,使数列
中存在某个连续
项的和是数列
中的一项,请证明.
已知函数
的反函数.定义:若对给定的实数
,函数
与
互为反函数,则称
满足"
和性质";若函数
与
互为反函数,则称
满足"
积性质".
(1)判断函数
是否满足"1和性质",并说明理由;
(2)求所有满足"2和性质"的一次函数;
(3)设函数
对任何
,满足"
积性质".求
的表达式.