已知椭圆 过点
过点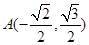 ,离心率为
,离心率为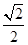 ,点
,点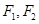 分别为其左右焦点.
分别为其左右焦点.
(1)求椭圆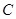 的标准方程;
的标准方程;
(2)若 上存在两个点
上存在两个点 ,椭圆上有两个点
,椭圆上有两个点 满足
满足 三点共线,
三点共线,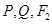 三点共线,且
三点共线,且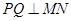 ,求四边形
,求四边形 面积的最小值.
面积的最小值.
(12分)设函数 满足条件f(-1+x)=f(-1-x),且关于x的不等式
满足条件f(-1+x)=f(-1-x),且关于x的不等式 的解集为
的解集为
(1)求函数f(x)的解析式;
(2)若 时,不等式
时,不等式 恒成立,求实数t的取值范围。
恒成立,求实数t的取值范围。
(12分)若函数y=lg(3-4x+x2)的定义域为M,.当x∈M时,
求f(x)=2x+2-3×4x的最值及相应的x的值.
(12分)已知函数f(x)=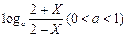
(1)判断f(x)的奇偶性,
(2)解不等式f(x)≥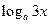
(12分)已知命题p: ∀x∈[1,2],x3-a≥0. 命题q:∃x0∈R,使得x+(a-1)x0+1<0.若 p为假,p且q为假,求实数a的取值范围.
p为假,p且q为假,求实数a的取值范围.
.(10分)已知集合A={x|>1,x∈R},B={x|x2-2 x-m<0},
x-m<0},
(1)当m=3时,求A∩(∁RB);
(2)若A∩B={x|-1<x<4},求实数m的值.