出租车司机小李某天下午的营运全是在东西走向的人民大街上行驶的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:
+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6.
(1)若小李下午出发地记为0,他将最后一名乘客送抵目的地时距出发地点有多远?
(2)若汽车耗油量为0.41升/ 千米,这天下午小李共耗油多少升?
如图,点A、E,是半圆周上的三等分点,直径=2,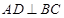 ,垂足为,连接交于,过作∥交于.
,垂足为,连接交于,过作∥交于.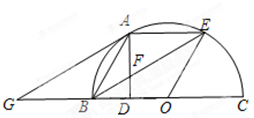
(1)判断直线与⊙的位置关系,并说明理由.
(2)求线段的长.
已知抛物线 经过点(3,0),(-1,0).
经过点(3,0),(-1,0).
(1)求抛物线的解析式;
(2)求抛物线的顶点坐标.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB•AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 的值.
的值.
如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾斜度由45°降为30°,已知原滑滑板的长为5米,点、、在同一水平地面上.
求:改善后滑滑板会加长多少?(精确到0.01)(参考数据: =1.414,
=1.414, =1.732,
=1.732, =2.449)
=2.449)
如图,在平面直角坐标系中,已知点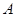 坐标为(2,4),直线x=2与
坐标为(2,4),直线x=2与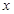 轴相交于点
轴相交于点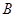 ,连结
,连结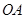 ,抛物线y=x
,抛物线y=x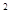
 从点
从点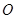 沿
沿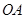 方向平移,与直线x=2交于点
方向平移,与直线x=2交于点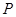 ,顶点
,顶点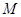 到
到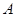 点时停止移动.
点时停止移动.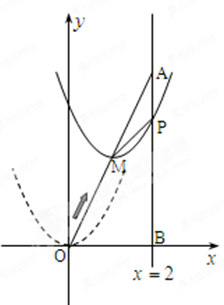
(1)求线段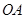 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点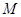 的横坐标为
的横坐标为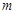 ,
,
①用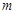 的代数式表示点
的代数式表示点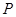 的坐标;
的坐标;
②当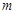 为何值时,线段
为何值时,线段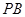 最短;
最短;
(3)当线段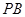 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点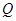 ,使△
,使△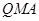 的面积与△
的面积与△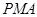 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点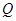 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.