(12分)△ABC在直角坐标系内的位置如图所示.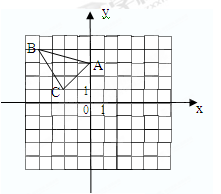
(1)分别写出A、B、C的坐标(3分)
(2)请在这个坐标系内画出△A1B1C1，使△A1B1C1与△ABC关于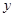
轴对称，并写出B1的坐标；(4分)
(3)请在这个坐标系内画出△A2B2C2，使△A2B2C2与△ABC关于原点对称，并写出A2的坐标；(5分)；
在△ABC中，
，
，直线
经过点
，且
于
，
于E.
（1）当直线绕点旋转到图1的位置时，求证： ①
≌
；②
.
（2）当直线绕点旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由.
如图，在△ABC中，AB=AC，点D、E、F分别在BC、AB、AC边上，且BE=CF，BD=CE.
（1）求证：△DEF是等腰三角形.
（2）当∠A=40°时，求∠DEF的度数.
和
是等边三角形,求证:
.
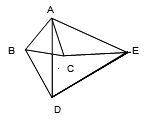
如图，A、D、F、B在同一直线上，AD=BF,AE=BC,且AE∥BC。
求证：
（1）△AEF≌△BCD；(2) EF∥CD.
