已知函数
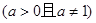 .
.
(1)求函数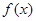 的定义域;
的定义域;
(2)若函数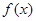 的最小值是
的最小值是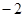 ,求实数
,求实数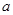 的值.
的值.
已知函数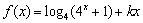 (
( )是偶函数
)是偶函数
(1)求 的值;
的值;
(2)设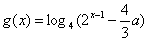 ,若函数
,若函数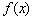 与
与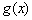 的图像有且只有一个公共点,求实数
的图像有且只有一个公共点,求实数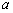 的取值范围
的取值范围
在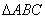 中,角
中,角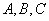 的对边分别为
的对边分别为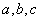 ,若
,若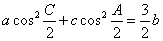 .
.
(Ⅰ)求证: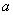 、
、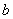 、
、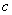 成等差数列;
成等差数列;
(Ⅱ)若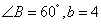 ,求
,求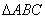 的面积.
的面积.
 中,
中,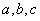 分别是角
分别是角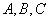 的对边,
的对边,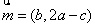 ,
,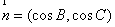 ,且
,且
(1)求角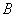 的大小;
的大小;
(2)设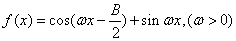 ,且
,且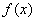 的最小正周期为
的最小正周期为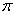 ,求
,求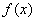 在
在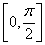 上的最大值和最小值,及相应的
上的最大值和最小值,及相应的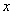 的值。
的值。
在等差数列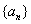 中,
中,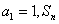 为前n项和,且满足
为前n项和,且满足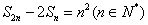
(1)求 及数列
及数列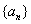 的通项公式;
的通项公式;
(2)记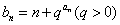 ,求数列
,求数列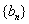 的前n项和
的前n项和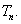
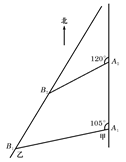
如图,甲船以每小时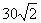 海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于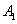 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西 的方向
的方向 处,此时两船相距20海里.当甲船航行20分钟到达
处,此时两船相距20海里.当甲船航行20分钟到达 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距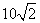 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?