(本小题满分12分)已知椭圆 的左、右焦点分别为
的左、右焦点分别为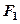 、
、 ,其中
,其中 也是抛物线
也是抛物线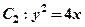 的焦点,M是
的焦点,M是 与
与 在第一象限的交点,且
在第一象限的交点,且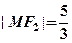 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知菱形ABCD的顶点A﹑C在椭圆 上,顶点B﹑D在直线
上,顶点B﹑D在直线 上,求直线AC的方程.
上,求直线AC的方程.
(12分)正项数列 的前
的前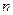 项和为
项和为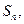 且
且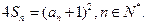
(1)试求数列 的通项公式;
的通项公式;
(2)设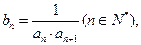 求数列
求数列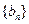 的前
的前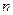 项和
项和
(本小题满分12分)在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA = 2,EC = 1.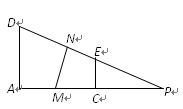

(Ⅰ)求点A到平面BDE的距离;
(Ⅱ)求二面角B–ED–A的正切值.
为援助玉树灾后重建,对某项工程进行竞标,共有6家企业参与竞标,其中A企业来自辽宁省,B、C两家企业来自福建省,D、E、F三家企业来自河北省,此项工程需要两家企业联合施工,假设每家企业中标的概率相同。
(1)企业E中标的概率是多少?
(2)在中标的企业中,至少有一家来自河北省的概率是多少?
在△ABC中,A、B、C的对边分别为a、b、c,且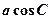 、
、 、
、 成等差数列.
成等差数列.
(Ⅰ)求B的值;
(Ⅱ)求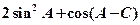 的范围。
的范围。