如图，已知二次函数图象的顶点坐标为C（1，0），直线
与该二次函数的图象交于A、B两点，其中A点的坐标为（3，4），B点在轴
上．
（1）求
的值及这个二次函数的关系式；
（2）P为线段AB上的一个动点（点P与A、B不重合），过P作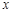
轴的垂线与这个二次函数的图象交于点E点，设线段PE的长为
，点P的横坐标为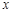，求与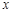之间的函数关系式，并写出自变量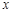的取值范围；
（3）D为直线AB与这个二次函数图象对称轴的交点，在线段AB上是否存在一点P，使得四边形DCEP是平行四边形？若存在，请求出此时P点的坐标；若不存在，请说明理由．
某市出租车收费标准为：起步价7元（即行驶距离不超过3km,都付7元车费），超过3km后，每增加1km，加收2.2元（不足1km,按1km计算）。某人乘坐了xkm（x为大于3的整数）路程。
（1）试用代数式表示他应付的车费；
（2）求当x=8km时的乘车费用；
（3）若此人付了29元车费，你能计算出此人乘坐的最远路程吗？
国庆前夕，新昌县质量技术监督局对该县某企业生产的罐头进行了抽检，从库中任意抽出样品20听进行检测，每听的质量超过标准质量部分记为正，不足部分记为负，记录如下表：
| 与标准质量的差（克） |
-8 |
-5 |
0 |
+2 |
+10 |
+12 |
| 听数 |
2 |
1 |
5 |
6 |
4 |
2 |
问这批样品平均每听质量比标准每听质量多或少几克？
．分解因式：a5－a3b2＋ab4
已知方程|2a＋3b＋1|＋（3a－b－1）2＝0，求a2＋2ab＋b2的值.
实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等。（1+1+1+1+1+4=9分）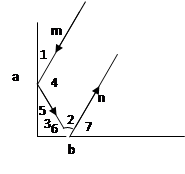
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=38°,则∠2=°,∠3=°。
(2)在(1)中,若∠1=55°,则∠3=°;若∠1=40°,则∠3=°。
(3)由(1)、(2),请你猜想:当两平面镜a、b的夹角∠3= ___°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.你能说明理由吗?