实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等。（1+1+1+1+1+4=9分）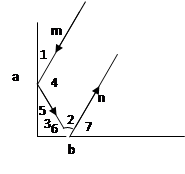
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=38°,则∠2= °,∠3= °。
(2)在(1)中,若∠1=55°,则∠3= °;若∠1=40°,则∠3= °。
(3)由(1)、(2),请你猜想:当两平面镜a、b的夹角∠3= ___°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.你能说明理由吗?
，已知线段CD=28㎝，求OP的长。
EB，F是BC的中点，BF=
AC=1.5㎝，求EF的长。
AB，反向延长AC到D，使DA=