如图，平面直角坐标系中，直线l分别交x轴、y轴于A、B两点（OA＜OB），且OA、OB的长分别是一元二次方程x2-（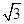
＋1）x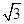＋＝0的两个根．点C在x轴负半轴上，且AB：AC＝1：2．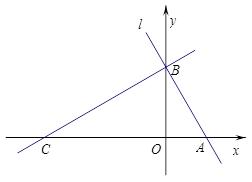 
（1）求A、C两点的坐标．
（2）若点M从点C出发，以每秒1个单位的速度沿射线CB运动，连接AM，设△ABM的面积为S，点M的运动时间为t，写出S关于t的函数关系式，并写出自变量的取值范围．
（3）点P是y轴上的点，在坐标平面内是否存在点Q，使以A、B、P、Q为顶点的四边形是菱形？若存在，请直接写出Q点的坐标；若不存在，说明理由．
如图有一座抛物线形拱桥，桥下面在正常水位是AB宽20m，水位上升3m就达到警戒线CD，这是水面宽度为10m。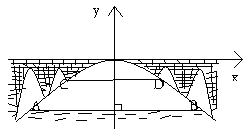
（1）在如图的坐标系中求抛物线的解析式。
（2）若洪水到来时，水位以每小时0.2m的速度上升，从警戒线开始，再持续多少小时才能到拱桥顶？
某单位于“三•八”妇女节期间组织女职工到温泉“星星竹海”观光旅游．下面是邻队与旅行社导游收费标准的一段对话：
邻队：组团去“星星竹海”旅游每人收费是多少？
导游：如果人数不超过25人，人均旅游费用为100元．
邻队：超过25人怎样优惠呢？
导游：如果超过25人，每增加1人，人均旅游费用降低2元，但人均旅游费用不得低于70元．
该单位按旅行社的收费标准组团浏览“星星竹海”结束后，共支付给旅行社2700元．
请你根 据上述信息，求该单位这次到“星星竹海”观光旅游的共有多少人？
某校团委准备举办学生绘画展览，为美化画面，在长为3 0cm、宽为20的矩形画面四周镶上宽度相等的彩纸，并使彩纸的面积恰好与原画面面积相等（如图），求彩纸的宽度．
如图，在平面直角坐标系中，已知点B（4，2），BA⊥x轴于A．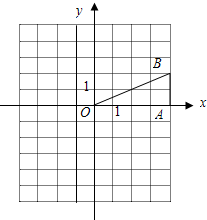
（1）画出将△OAB绕原点逆时针旋转90°后所得的△OA1B1，并写出点A1、B1的坐标；
（2）△OAB关于原点O的中心对称图形，并写出点A、B对称点的坐标.．
如图，PA，PB是⊙O的切线，点A，B为切点，AC是⊙O的直径，∠ACB=70°．求∠P的度数．