汽车发动机的功率为60KW,汽车的质量为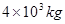 。汽车在足够长的水平路面从静止以0.6m/s2的加速度做匀加速直线运动。(已知汽车在行驶中所受路面阻力恒定为重力的0.1倍,g取10m/s2)求:
。汽车在足够长的水平路面从静止以0.6m/s2的加速度做匀加速直线运动。(已知汽车在行驶中所受路面阻力恒定为重力的0.1倍,g取10m/s2)求:
(1)汽车在水平路面能达到的最大速度vm1
(2)汽车在水平路面做匀加速运动能维持多长时间
如图所示,在海滨游乐场里有一种滑沙运动。某人坐在滑板上从斜坡的高处A点由静止开始滑下,滑到斜坡底端B点后,沿水平的滑道再滑行一段距离到C点停下来。若人和滑板的总质量m =" 60.0" kg,滑板与斜坡滑道和水平滑道间的动摩擦因数均为μ = 0.50,斜坡的倾角θ = 37°(sin37° = 0.6,cos37° = 0.8),斜坡与水平滑道间是平滑连接的,整个运动过程中空气阻力忽略不计,重力加速度g取10 m/s2。求: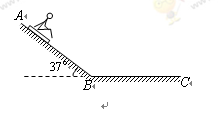
(1)人从斜坡上滑下的加速度大小为多少
(2)若AB的长度为25m,求BC的长度为多少
如图甲所示,在光滑绝缘的水平桌面上建立一xoy坐标系,平面处在周期性变化的电场和磁场中,电场和磁场的变化规律如图乙所示(规定沿+y方向为电场强度的正方向,竖直向下为磁感应强度的正方向).在t=0时刻,一质量为m=10g、电荷量为q=0.1C的带电金属小球自坐标原点O处,以v0=2m/s的速度沿x轴正方向射出.已知E0=0.2N/C、B0=0.2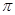 T.求:
T.求: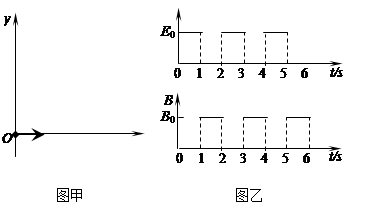
(1)t=1s末速度的大小和方向;
(2)1s~2s内,金属小球在磁场中做圆周运动的半径和周期;
(3)试求出第3秒末小球所在位置的坐标。
如图,半径R=0.9m的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B与长为L=1m的水平面相切于B点,BC离地面高h=0.45m,C点与一倾角为θ=300的光滑斜面连接,质量m=1.0kg的小滑块从圆弧顶点D由静止释放,已知滑块与水平面间的动摩擦因数μ=0.1.,取g=10m/s2.求: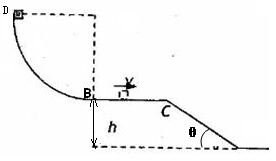
(1)小滑块刚到达圆弧的B点时对圆弧的压力;
(2)小滑块到达C点时速度的大小;
(3)小滑块从C点运动到地面所需的时间。
为了研究过山车的原理,物理小组提出了下列的设想:取一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的。其中AB与BC轨道以微小圆弧相接,如图所示。一个小物块以初速度v0=4.0m/s,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下。已知物块与倾斜轨道的动摩擦因数u=0.50(g取10m/s2,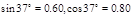 )求:
)求: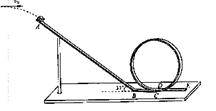
(1)小物块的抛出点和A点的高度差;
(2)要使小物块不离开轨道,并从水平轨道DE滑出,求竖直圆弧轨道的半径应该满足什么条件;
(3)为了让小物块不离开轨道,并且能够滑回倾斜轨道AB,则竖直圆轨道的半径应该满足什么条件。