如图所示,左侧为一个半径为R的半球形的碗固定在水平桌面上,碗口水平, O点为球心,碗的内表面及碗口光滑。右侧是一个固定光滑斜面,斜面足够长,倾角θ=30°。一根不可伸长的不计质量的细绳跨在碗口及光滑斜面顶端的光滑定滑轮两端上,线的两端分别系有可视为质点的小球m1和m2,且m1>m2。开始时m1恰在右端碗口水平直径A处, m2在斜面上且距离斜面顶端足够远,此时连接两球的细绳与斜面平行且恰好伸直。当m1由静止释放运动到圆心O的正下方B点时细绳突然断开,不计细绳断开瞬间的能量损失。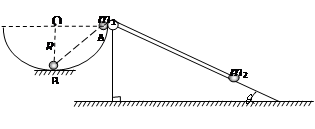
(1)求小球m2沿斜面上升的最大距离s;
(2)若已知细绳断开后小球m1沿碗的内侧上升的最大高度为R/2,求 =?
=?
两个质量都是M=0.4kg的砂箱A、B并排放在光滑的水平桌面上,一颗质量为m=0.1kg的子弹以v0=140m/s的水平速度射向A,如图所示.射穿A后,进入B并同B一起运动,测得A、B落点到桌边缘的水平距离sA:sB=1:2,求子弹在砂箱A、B中穿行时系统一共产生的热量Q.
如图所示,内壁光滑半径为R的圆形轨道,固定在竖直平面内.质量为m1的小球静止在轨道最低点,另一质量为m2的小球(两小球均可视为质点)从内壁上与圆心O等高的位置由静止释放,运动到最低点时与m1发生碰撞并粘在一起.求: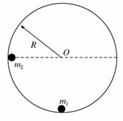
(1)小球m2刚要与m1发生碰撞时的速度大小;
(2)碰撞后,m1、m2能沿内壁运动所能达到的最大高度(相对碰撞点).
如图所示,在光滑水平面上有两个并排放置的木块A和B,已知mA="500" g,mB="300" g,有一质量为80 g的小铜球C以25 m/s的水平初速开始,在A表面滑动,由于C和A,B间有摩擦,铜块C最后停在B上,B和C一起以2.5 m/s的速度共同前进,求:
(1)木块A的最后速度vA′;
(2)C在离开A时速度vC′.
如图所示,光滑的水平地面上有一木板,其左端放有一重物,右方有一竖直的墙.重物质量为木板质量的2倍,重物与木板间的动摩擦因数为μ.使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短.求木板从第一次与墙碰撞到再次碰撞所经历的时间.设木板足够长,重物始终在木板上.重力加速度为g.
质量为100 kg的甲车连同质量为50 kg的人一起以2 m/s的速度在光滑水平上向前运动,质量为150 kg的乙车以7 m/s的速度由后面追来.为了避免相碰,当两车靠近时甲车上的人至少应以多大的水平速度跳上乙车?