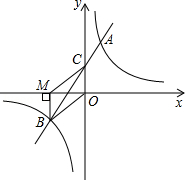
图①、图②分别由两个长方形拼成.
(1)观察思考:
(Ⅰ)图①的两个长方形的面积和S1= ;
A.a2+b2 B.a2+ab C.b2-ab D.a2-b2
(Ⅱ)图②的两个长方形的面积和S2= ;
A.a(a-b) B.b(a-b) C.(a+b)(a-b) D.ab(a+b)
(2)过程探索:
| a的取值 |
b的取值 |
S1 |
S2 |
| a=5 |
b=2 |
|
|
| a=7.5 |
b=4.5 |
|
|
猜想归纳:S1 S2(填“>”或“=”或“<”)
结论应用:10000.52-9999.52(写出具体计算过程)
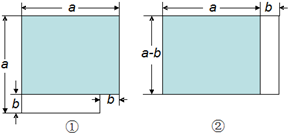
在 中, , 是 内一点,连接 , ,在 左侧作 ,使 ,以 和 为邻边作 ,连接 , .
(1)若 , .
①如图1,当 , , 三点共线时, 与 之间的数量关系为 .
②如图2,当 , , 三点不共线时,①中的结论是否仍然成立?请说明理由.
(2)若 , , ,且 , , 三点共线,求 的值.
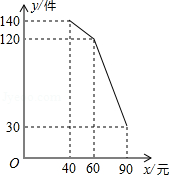
某商场销售一种商品的进价为每件30元,销售过程中发现月销售量 (件 与销售单价 (元 之间的关系如图所示.
(1)根据图象直接写出 与 之间的函数关系式.
(2)设这种商品月利润为 (元 ,求 与 之间的函数关系式.
(3)这种商品的销售单价定为多少元时,月利润最大?最大月利润是多少?
如图,在 中, , 是 上一点,过 , , 三点的 交 于点 ,连接 , ,点 是线段 上的一点,连接 ,其中 .
(1)求证: 是 的切线.
(2)若 是 的中点, , ,求 的长.
如图为某海域示意图,其中灯塔 的正东方向有一岛屿 .一艘快艇以每小时 的速度向正东方向航行,到达 处时测得灯塔 在东北方向上,继续航行 ,到达 处时测得灯塔 在北偏东 方向上,同时测得岛屿 恰好在 处的东北方向上,此时快艇与岛屿 的距离是多少?(结果精确到 .参考数据: , ,

如图,在平面直角坐标系中,一次函数 的图象与 轴交于点 ,与反比例函数 的图象交于 , 两点,点 在第一象限,纵坐标为4,点 在第三象限, 轴,垂足为点 , .
(1)求反比例函数和一次函数的解析式.
(2)连接 , ,求四边形 的面积.