欧拉公式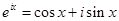 (
(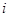 为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”,根据欧拉公式可知,
为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”,根据欧拉公式可知,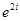 表示的复数在复平面中位于( )
表示的复数在复平面中位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
已知两条直线 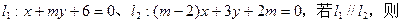 m的值为 ()
m的值为 ()
| A.m=-1 | B.m="3" | C.m=-1或m="3" | D.m=-3或m=1 |
抛物线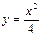 的焦点坐标是()
的焦点坐标是()
A.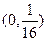 |
B.(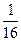 ,0) ,0) |
C.(1,0) | D.(0,1) |
双曲线 的渐近线方程是 ()
的渐近线方程是 ()
A.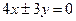 |
B. |
C.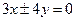 |
D. |
已知函数定义域为D的函数f(x),如果对x D,存在正数k,有|f(x)|≤k|x|成立,则称函数f(x)是D上的“倍约束函数”,已知下列函数:(1)f(x)=2x; (2)f(x)=Sin(x+
D,存在正数k,有|f(x)|≤k|x|成立,则称函数f(x)是D上的“倍约束函数”,已知下列函数:(1)f(x)=2x; (2)f(x)=Sin(x+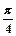 );(3)f(x)=
);(3)f(x)=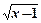 ;(4)f(x)=
;(4)f(x)=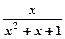 ;其中是“倍约束函数”的是()
;其中是“倍约束函数”的是()
| A.(1)(3)(4) | B.(1)(2) | C.(3)(4) | D.(2)(3)(4) |
实数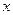 满足
满足 ,则
,则 的值为()
的值为()
A.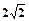 |
B.3 | C.4 | D.与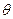 有关 有关 |