如图, 为一直角三角形草坪,其中
为一直角三角形草坪,其中 ,
, 米,
米, 米,为了重建草坪,设计师准备了两套方案:
米,为了重建草坪,设计师准备了两套方案:
方案一:扩大为一个直角三角形,其中斜边 过点
过点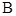 ,且与
,且与 平行,
平行, 过点
过点 ,
, 过点
过点 ;
;
方案二:扩大为一个等边三角形,其中 过点
过点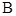 ,
, 过点
过点 ,
, 过点
过点 .
.
(1)求方案一中三角形 面积
面积 的最小值;
的最小值;
(2)求方案二中三角形 面积
面积 的最大值.
的最大值.
在已知函数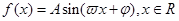 (其中
(其中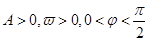 )的图象与
)的图象与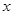 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为 ,且图象上一个最低点为
,且图象上一个最低点为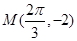 ,
,
(1).求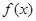 的解析式 (2).当
的解析式 (2).当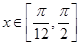 时,求
时,求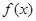 的值域。
的值域。
设函数 ,其中
,其中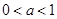 ,
,
(1)证明: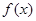 是
是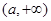 上的减函数;
上的减函数;
(2)解不等式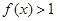
在 中,内角
中,内角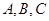 对边的边长分别是
对边的边长分别是 ,已知
,已知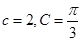 ,
,
(1)若 的面积等于
的面积等于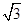 ,求
,求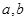 ;
;
(2)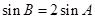 ,求
,求 的面积。
的面积。
(本小题满分10分)选修4-5:不等式选讲
设函数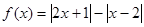 .
.
(Ⅰ)求不等式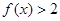 的解集;
的解集;
(Ⅱ)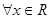 ,使
,使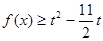 ,求实数的取值范围.
,求实数的取值范围.
(本小题满分13分)设函数f(x)=x3+ax2-a2x+m(a>0).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在x∈[-1,1]内没有极值点,求a的取值范围;
(Ⅲ)若对任意的a∈[3,6],不等式f(x)≤1在x∈[-2,2]上恒成立,求m的取值范围.