(本小题满分12分)
已知等差数列 的公差为
的公差为 ,前
,前 项和为
项和为 ,且
,且 .
.
(1)求数列 的通项公式
的通项公式 与前
与前 项和
项和 ;
;
(2)将数列 的前四项抽取其中一项后,剩下三项按原来顺序恰为等比数列
的前四项抽取其中一项后,剩下三项按原来顺序恰为等比数列 的前三项,记数列
的前三项,记数列 的前
的前 项和为
项和为 ,若存在
,若存在 ,使得对任意
,使得对任意 ,总有
,总有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知椭圆 :
: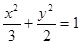 的左焦点为
的左焦点为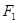 ,右焦点为
,右焦点为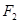 .
.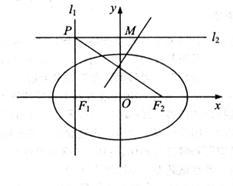
(Ⅰ)设直线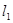 过点
过点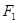 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线 垂直
垂直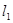 于点P,线段
于点P,线段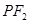 的垂直平分线交
的垂直平分线交 于点M,求点M的轨迹
于点M,求点M的轨迹 的方程;
的方程;
(Ⅱ)设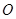 为坐标原点,取曲线
为坐标原点,取曲线 上不同于
上不同于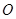 的点
的点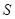 ,以
,以 为直径作圆与
为直径作圆与 相交另外一点
相交另外一点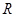 ,求该圆的面积最小时点
,求该圆的面积最小时点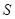 的坐标.
的坐标.
已知轴对称平面五边形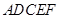 (如图1),
(如图1),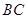 为对称轴,
为对称轴, ,
, ,
, ,将此图形沿
,将此图形沿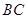 折叠成直二面角,连接
折叠成直二面角,连接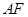 、
、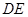 得到几何体(如图2).
得到几何体(如图2).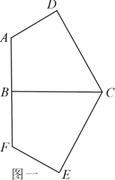
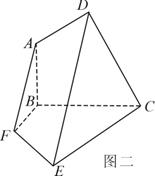
(Ⅰ)证明: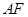 ∥平面
∥平面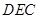 ;
;
(Ⅱ)求二面角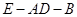 的余弦值.
的余弦值.
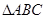 中,角
中,角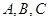 所对的边分别为
所对的边分别为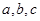 且
且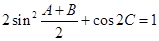 .
.
(Ⅰ)求角的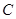 大小;
大小;
(Ⅱ)若向量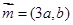 ,向量
,向量 ,
,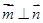 ,
,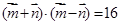 ,求
,求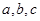 的值.
的值.
已知函数 (
( ).
).
(Ⅰ)若 的定义域和值域均是
的定义域和值域均是 ,求实数
,求实数 的值;
的值;
(Ⅱ)若 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的 ,
, ,总有
,总有 ,求实数
,求实数 的取值范围.
的取值范围.
已知函数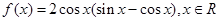 .
.
(Ⅰ)求函数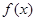 图像的对称中心;
图像的对称中心;
(Ⅱ)求函数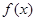 在区间
在区间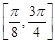 上的最小值和最大值.
上的最小值和最大值.