如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径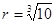 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.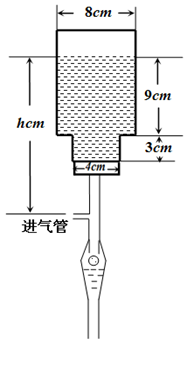
(1)如果瓶内的药液恰好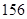 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?
(2)在条件(1)下,设输液开始后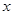 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为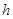 (单位:厘米),已知当
(单位:厘米),已知当 时,
时, .试将
.试将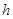 表示为
表示为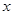 的函数.(注:
的函数.(注: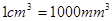 )
)
定义:对于函数 ,若存在非零常数
,若存在非零常数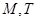 ,使函数
,使函数 对于定义域内的任意实数
对于定义域内的任意实数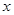 ,都有
,都有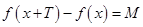 ,则称函数
,则称函数 是广义周期函数,其中称
是广义周期函数,其中称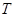 为函数
为函数 的广义周期,
的广义周期,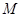 称为周距.
称为周距.
(1)证明函数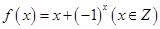 是以2为广义周期的广义周期函数,并求出它的相应周距
是以2为广义周期的广义周期函数,并求出它的相应周距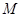 的值;
的值;
(2)试求一个函数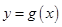 ,使
,使 (
(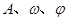 为常数,
为常数,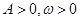 )为广义周期函数,并求出它的一个广义周期
)为广义周期函数,并求出它的一个广义周期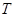 和周距
和周距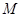 ;
;
(3)设函数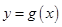 是周期
是周期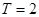 的周期函数,当函数
的周期函数,当函数 在
在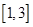 上的值域为
上的值域为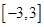 时,求
时,求 在
在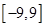 上的最大值和最小值.
上的最大值和最小值.
已知椭圆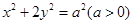 的一个顶点和两个焦点构成的三角形的面积为4.
的一个顶点和两个焦点构成的三角形的面积为4.
(1)求椭圆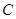 的方程;
的方程;
(2)已知直线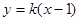 与椭圆
与椭圆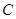 交于
交于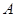 、
、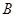 两点,试问,是否存在
两点,试问,是否存在 轴上的点
轴上的点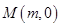 ,使得对任意的
,使得对任意的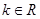 ,
,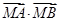 为定值,若存在,求出
为定值,若存在,求出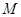 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.
如图所示,某旅游景点有一座风景秀丽的山峰,山上有一条笔直的山路BC和一条索道AC,小王和小李打算不坐索道,而是花2个小时的时间进行徒步攀登.已知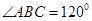 ,
, ,
,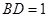 (千米),
(千米),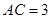 (千米).假设小王和小李徒步攀登的速度为每小时1200米,请问:两位登山爱好者能否在2个小时内徒步登上山峰.
(千米).假设小王和小李徒步攀登的速度为每小时1200米,请问:两位登山爱好者能否在2个小时内徒步登上山峰.
(即从B点出发到达C点)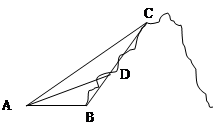
如图,△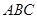 中,
中,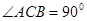 ,
,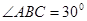 ,
,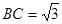 ,在三角形内挖去一个半圆(圆心
,在三角形内挖去一个半圆(圆心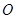 在边
在边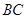 上,半圆与
上,半圆与 、
、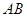 分别相切于点
分别相切于点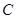 、
、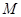 ,与
,与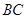 交于点
交于点 ),将△
),将△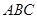 绕直线
绕直线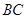 旋转一周得到一个旋转体.
旋转一周得到一个旋转体.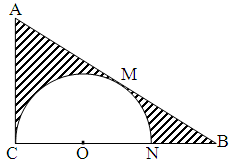
(1)求该几何体中间一个空心球的表面积的大小;
(2)求图中阴影部分绕直线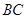 旋转一周所得旋转体的体积.
旋转一周所得旋转体的体积.
已知抛物线 的准线与
的准线与 轴交于点
轴交于点 ,过点
,过点 作圆
作圆 的两条切线,切点为
的两条切线,切点为
(Ⅰ)求抛物线E的方程;
(Ⅱ)过抛物线E上的点N作圆C的两条切线,切点分别为 若
若 为原点)三点共线,求点N的坐标.
为原点)三点共线,求点N的坐标.