已知 是最大的负整数,b是多项式
是最大的负整数,b是多项式 的次数,c是单项式
的次数,c是单项式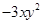 的系数,且
的系数,且 、b、c分别是点A、B、C在数轴上对应的数.
、b、c分别是点A、B、C在数轴上对应的数.
(1)求 、b、c的值,并在数轴上标出点A、B、C.
、b、c的值,并在数轴上标出点A、B、C.
(2)若动点P、Q同时从A、B出发沿数轴负方向运动,点P的速度是每秒1个单位长度,点Q的速度是每秒 个单位长度,求运动几秒后,点Q可以追上点P?
个单位长度,求运动几秒后,点Q可以追上点P?
(3)在数轴上找一点M,使点M到A、B、C三点的距离之和等于12,请直接写出所有点M对应的数.(不必说明理由).
某宾馆有30个房间供游客住宿,当每个房间的房价为每天120元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于210元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
如图,△ABC中,AB=AC,作以AB为直径的⊙O与边BC交于点D,过点D作⊙O的切线,分别交AC、AB的延长线于点E、F.
(1)求证:EF⊥AC;
(2)若BF=2,CE=1.2,求⊙O的半径.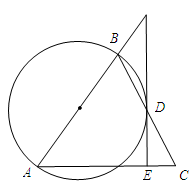
PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据PM2.5检测网的空气质量新标准,从德州市2013年全年每天的PM2.5日均值标准值(单位:微克/立方米)监测数据中随机地抽取25天的数据作为样本,并根据检测数据制作了尚不完整的频数分布表和条形图:

(1)求出表中m,n,a的值,并将条形图补充完整;
(2)以这25天的PM2.5日均值来估计该年的空气质量情况,估计该年(365天)大约有多少天的空气质量达到优或良;
(3)请你结合图表评价一下我市的空气质量情况.
如图,已知矩形OABC的A点在x轴上,C点在y轴上,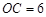 ,
,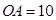 .
.
(1)在BC边上求作一点E,使OE=OA;(保留作图痕迹,不写画法)
(2)求出点E的坐标.
化简求值: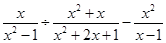 ,其中
,其中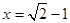 .
.