兰新铁路的通车，圆了全国人民的一个梦，坐上火车去观赏青海门源百里油菜花海，感受大美青海独特的高原风光，暑假某校准备组织学生、老师到门源进行社会实践，为了便于管理，师生必须乘坐在同一列高铁上，根据报名人数，若都买一等座单程火车票需2340元，若都买二等座单程火车票花钱最少，则需1650元：
西宁到门源的火车票价格如下表
| 运行区间 |
票价 |
|
|
| 上车站 |
下车站 |
一等座 |
二等座 |
| 西宁 |
门源 |
36元 |
30元 |
（1）参加社会实践的学生、老师各有多少人？
（2）由于各种原因，二等座火车票单程只能买x张（参加社会实践的学生人数＜x＜参加社会实践的总人数），其余的须买一等座火车票，在保证每位参与人员都有座位坐并且总费用最低的前提下，请你写出购买火车票的总费用（单程）y与x之间的函数关系式．
如图，八一广场要设计一个矩形花坛，花坛的长、宽分别为200 m、
120 m，花坛中有一横两纵的通道，横、纵通道的宽度分别为3x m、2x m．
（1）用代数式表示三条通道的总面积S；当通道总面积为花坛总面积的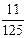
时，求横、纵通道的宽分别是多少？
（2）如果花坛绿化造价为每平方米3元，通道总造价为3168 x元，那么横、纵通道的宽分别为多少米时，花坛总造价最低？并求出最低造价．
（以下数据可供参考：852 = 7225，862 = 7396，872 = 7569）
如图，已知正比例函数y = ax（a≠0）的图象与反比例函致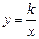
（k≠0）的图象的一个交点为A（－1，2－k2），另—个交点为B，且A、B关于原点O对称，D为OB的中点，过点D的线段OB的垂直平分线与x轴、y轴分别交于C、E．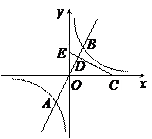
（1）写出反比例函数和正比例函数的解析式；
（2）试计算△COE的面积是△ODE面积的多少倍．
绵阳农科所为了考察某种水稻穗长的分布情况，在一块试验田里随机抽取了50个谷穗作为样本，量得它们的长度（单位：cm）．对样本数据适当分组后，列出了如下频数分布表：
| 穗长 |
4.5≤x＜5 |
5≤x＜5.5 |
5.5≤x＜6 |
6≤x＜6.5 |
6.5≤x＜7 |
7≤x＜7.5 |
| 频数 |
4 |
8 |
12 |
13 |
10 |
3 |
（1）在图1、图2中分别出频数分布直方图和频数折线图；
（2）请你对这块试验田里的水稻穗长进行分析；并计算出这块试验田里穗长在5.5≤x＜7范围内的谷穗所占的百分比．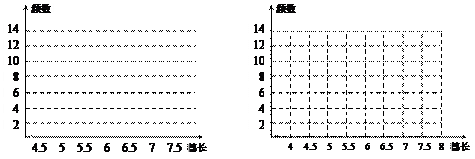
图1图2
已知关于x的一元二次方程x2 = 2（1－m）x－m2 的两实数根为x1，x2．
（1）求m的取值范围；
（2）设y = x1 + x2，当y取得最小值时，求相应m的值，并求出最小值．
如图，抛物线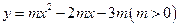
与
轴交于
两点，与
轴交于
点.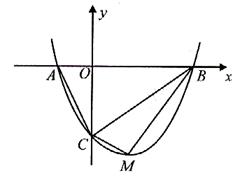
（1）请求出抛物线顶点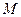
的坐标（用含
的代数式表示），两点的坐标；
（2）经探究可知，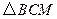
与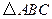
的面积比不变，试求出这个比值；
（3）是否存在使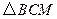为直角三角形的抛物线？若存在，请求出；如果不存在，请说明
理由.