如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)
(1)数轴上点B对应的数是______.
(2)经过几秒,点M、点N分别到原点O的距离相等?
(3)当点M运动到什么位置时,恰好使AM=2BN?
(本题7分)如图, 分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。
分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。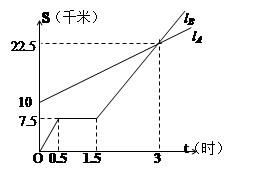
(1)B出发时与A相距千米。
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是小时。
(3)B出发后小时与A相遇。
(4)若B的自行车不发生故障,保持出发时的速度前进,小时与A相遇?相遇点离B的出发点千米?在图中表示出这个相遇点C。
(5)A行走的路程S与时间t的函数关系式为。
(本题6分)在一次消防演习中,消防员架起一架25米长的云梯AB,如图斜靠在一面墙上,梯子底端B离墙角C的距离为7米。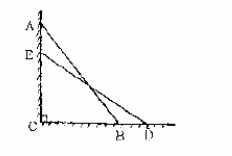
(1)求这个梯子的顶端距地面的高度AC是多少?
(2)如果消防员接到命令,按要求将梯子底部在水平方向滑 动后停在DE的位置上(云梯长度不变),测得BD长为8米,那么云梯的顶部在下滑了多少米?
(本题7分)如图,方格纸中的每个小方格都是边长为1的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,A(-1,5),B(-1,0),C(-4,3).
(1)画出△ABC关于y轴对称的△A1B1C1;(其中A1、B1、C1是A、B、C的对应点,不写画法)
(2)写出A1、B1、C1的坐标;
(3)求出△A1B1C1的面积.
(本题4分)已知  求x的值。
求x的值。
如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个 小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,…,请你根据以上操作方法得到的正方形的个数的规律完成各题.
(1)将下表填写完整;
(2)an =()(用含n的代数式表示);
(3)按照上述方法,能否得到2015个正方形?如果能,请求出n;如果不能,请简述理由.