观察下列每对数在数轴上的对应点之间的距离：4与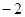
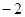，3与5，与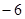
，
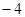与3．并回答下列各题：
（1）你能发现所得距离与这两个数的差的绝对值有什么关系吗？ 答： ．
（2）若数轴上的点A表示的数为x，点B表示的数为－1，则A与B两点间的距离可以表示为 ．
（3）结合数轴探求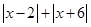
的最小值，并说明取得最小值时x的取值范围．
（1）已知关于x的一次函数y=(2k-3)x+k-1的图像与y轴交点在x轴的上方，且y随x的增大而减小，求k的取值范围；
（2）已知函数y=(4m-3)x是正比例函数，且y随x的增大而增大，求m的取值范围．
对于任何实数x，点M(x，x-1)一定不在第几象限？
在直角坐标系中，有四个点A(-8，3)，B(-4，5)，C(0，n)，D(m，0)，当四边形ABCD的周长最短时，求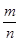
的值.
求证：不论k为何值，一次函数(2k-1)x- (k+3)y-(k-11)=0的图像恒过一定点.
如图，在等边△ABC中，AD⊥BC于点D，一个直径与AD相等的圆与BC相切于点E，与AB相切于点F，连接EF。
（1）判断EF与AC的位置关系（不必说明理由）；；
（2）如图（2），过E作BC的垂线，交圆于G，连接AG，判断四边形ADEG的形状，并说明理由。
（3）求证：AC与GE的交点O为此圆的圆心．