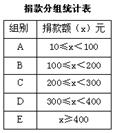
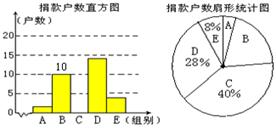
2011年3月10日,云南省盈江县发生5.8级地震,地震灾情牵动全国人民的心.某社区响应恩施州政府的号召,积极组织社区居民为灾区人民献爱心活动.为了解该社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图8所示的不完整统计图.已知A、B两组捐款户数比为1:5,请结合图中相关数据回答下列问题.A组的频数是多少?本次调查样本的容量是多少?
求出C组的频数并补全直方图.
若该社区有500户住户,请估计捐款不少于300元的户数是多少?
先化简,  ,再选一个你喜欢的数代入求值:
,再选一个你喜欢的数代入求值:
计算: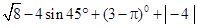
如图,A、B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y个单位长度沿y轴的正方向运动.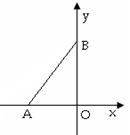
若∣x+2y-5∣+∣2x-y∣=0,试分别求出运动1秒钟时,
A、B两点的坐标.设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P,
问:点A、B在运动的过程中,∠P的大小是否会发生变化?若不发
生变化,请求出其值;若发生变化,请说明理由
已知如图,在△ABC中,AD、AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°求∠DAE的度数。
试写出∠DAE与∠B、∠C之间关系?(不必证明)
