甲乙两名同学做摸球游戏，他们把三个分别标有1，2，3的大小和形状完全相同的小球放在一个不透明的口袋中．
（1）求从袋中随机摸出一球，标号是1的概率；
（2）从袋中随机摸出一球后放回，摇匀后再随机摸出一球，若两次摸出的球的标号之和为偶数时，则甲胜；若两次摸出的球的标号之和为奇数时，则乙胜；试分析这个游戏是否公平？请说明理由．
如图，三角形ABC中，BE平分
ABC，1=2，C=50°，求AED的度数
计算：（1）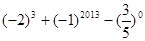
；（2）（3a＋5b）（－3a－8b）
解方程组：（1）
；（2）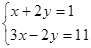
如图所示，已知∠1=∠2，∠3=85°，求∠4的度数．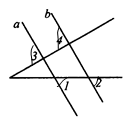
解：∵∠1=∠2（）
∴a∥b（）
∴∠3=∠4（）
∵∠3=85°（）
∴∠4=85°
如图(1)线段AB、CD相交于点O,连接AD、CB．如图(2),在图(1)的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．
试解答下列问题：
(1)在图(1)中,请直接写出∠A、∠B、∠C、∠D之间的等量关系；
(2)在图(2)中,若∠D=40°,∠B=30°,试求∠P的度数；（写出解答过程）