一转动装置如图甲所示，两根足够长轻杆OA、OB固定在竖直轻质转轴上的O点，两轻杆与转轴间夹角均为30°，小球a、b分别套在两杆上，小环c套在转轴上，球与环质量均为m，c与a、b间均用长为L的细线相连，原长为L的轻质弹簧套在转轴上，且与轴上P点、环c相连。当装置以某一转速转动时，弹簧伸长到
，环c静止在O处，此时弹簧弹力等于环的重力，球、环间的细线刚好拉直而无张力。弹簧始终在弹性限度内，忽略一切摩擦和空气阻力，重力加速度为g。求：
（1）细线刚好拉直而无张力时，装置转动的角速度ω1
（2）如图乙所示，该装置以角速度ω2（未知）匀速转动时，弹簧长为L/2，求此时杆对小球的弹力大小；
（3）该装置转动的角速度由ω1缓慢变化到ω2，求该过程外界对转动装置做的功。
有一匝数为10匝的正方形线圈，边长为20 cm，线圈总电阻为1 Ω，线圈绕OO′轴以10π rad/s的角速度匀速转动，如图所示，垂直于线圈平面(纸面)向里的匀强磁场的磁感应强度为0.5 T。问：(从如图所示位置开始计时)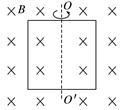
(1)该线圈产生的交变电流的电动势峰值和电流的峰值分别为多少？
(2)线圈从图示位置转过60°时，感应电动势的瞬时值是多大？
(3)写出感应电动势随时间变化的瞬时值表达式。
如图所示 ，C是静止放在光滑的水平面上的一块木板，木板的质量为2m。小木块B以2v0的初速度水平向右从木板左端滑上木板。当B与C相对静后，小木块A以v0的初速度水平向右从木板左端滑上木板。小木块A和B质量均为m，它们与木板间的动摩擦因数均为μ，且木板足够长，重力加速度为g。求：
(1)小木块B的最终速度；
(2)小木块A与小木块B最终距离。
如图甲所示，在一个正方形金属线圈区域内存在着磁感应强度B随时间变化的匀强磁场，磁场的方向与线圈平面垂直．金属线圈所围的面积S＝200 cm2，匝数n＝1 000，线圈电阻r＝1.0 Ω.线圈与电阻R构成闭合回路，电阻的
阻值R ＝4.0 Ω.匀强磁场的磁感应强度随时间变化的情况如
图乙所示，求：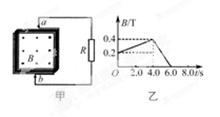
(1) 在t＝2.0 s时通过电阻R的感应电流的大小；
(2) 在t＝5.0 s时刻，线圈端点a、b间的电压；
质量为2 kg的平板车B上表面水平,原来静止在光滑水平面上,平板车一端静止着一块质量为2 kg的物体A,一颗质量为0.01 kg的子弹以600 m/s的速度水平瞬间射穿A后,速度变为100 m/s。 
(1)A的最大速度;
(2)若A不会滑离B,B的最大速度是多少?
一理想降压变压器，原线圈上所加电压为11 kV，副线圈通过输电导线向用户供电，输电导线的总电阻R＝0.05 Ω，用户的用电器(假设是纯电阻)得到的电压为220 V、消耗的电功率为44 kW.求变压器原、副线圈的匝数比n1∶n2.