磁强计的原理如图所示,电路中有一段金属导体,它的横截面积的边长等于a的正方形,放在沿x正方向的匀强磁场中,导体中通有沿y方向、电流强度为I的电流,已知金属导体单位体积中的自由电子数为n,电子电量为e,金属导体导电过程中,自由电子所做的定向移动可以认为是匀速运动,测出导体上下两侧面间的电势差为U.求: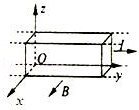
(1)导体上、下侧面哪个电势较高?
(2)磁场的磁感应强度是多大?
如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C;方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量m=6.64×10-27kg,电荷量q=3.2×10-19C,初速度v=3.2×106m/s.
(sin37°=0.6,cos37°=0.8)求:
(1)α粒子在磁场中作圆周运动的轨道半径R;
(2)金箔cd被α粒子射中区域的长度L;
(3)设打在金箔上d端离cd中心最远的α粒子穿出金箔进入电场,在电场中运动通过N点,SN⊥ab且SN=40cm,则此α粒子从金箔上穿出时,损失的动能△EK为多少?
质为m=2kg的物体静止在水平面上,它与地面之间的动摩擦因数μ=0.5,现在对物体施加以如图所示的拉力F=10N,与水平方向夹角θ=37°(sin37°=0.6),经过t=10s后撤去力F,再经一段时间,物体又静止。(g取10m/s2)求:
(1)物体运动过程中最大速度的大小;
(2)物体运动的总位移的大小.
如图所示,质量m=2kg的滑块(可视为质点),以v0=5m/s的水平初速度滑上静止在光滑水平面的平板小车,若平板小车质量M=3kg,长L=4.8m。滑块在平板小车上滑移1.5s后相对小车静止。求:
i.滑块与平板小车之间的滑动摩擦系数μ;
ii. 若要滑块不滑离小车,滑块的初速度不能超过多少。(g取10m/s2)
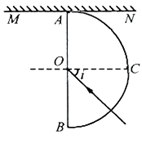
如图所示为某种透明介质的截面图,ACB为半径R=10cm的二分之一圆弧,AB与水平面屏幕MN垂直并接触于A点。由红光和紫光两种单色光组成的复色光射向圆心O,在AB分界面上的入射角i=45°,结果在水平屏幕MN上出现两个亮斑。已知该介质对红光和紫光的这首率分别为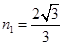 ,
, 。
。
i. 判断在AM和AN两处产生亮斑的颜色;
ii. 求两个亮斑间的距离。
如图所示,开中向上竖直放置的内壁光滑气缸,其侧壁是绝热的,底部导热,内有两个质量均为m的密闭活塞,活塞A导热,活塞B绝热,将缸内理想气体分成I、II两部分。初状态整个装置静止不动处于平衡,I、II两部分气体的长度均为l0,温度均为T0.设外界大气压强p0保持不变,活塞横截面积为S,且mg=p0S,环境温度保持不变。求: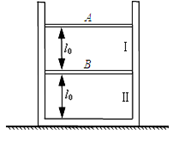
i. 在活塞A上逐渐添加铁砂,当铁砂质量等于m时,两活塞在某位置重新处于平衡,活塞B下降的高度;
ii. 现只对II气体缓慢加热,使活塞A回到初始位置,此时II气体的温度。