质量均为m的物体A和B分别系在一根不计质量的细绳两端,绳子跨过固定在倾角为30°的光滑斜面顶端的定滑轮上,斜面固定在水平地面上。开始时把物体B拉到斜面底端,这时物体A离地面的高度为0.8m,如图所示。若摩擦力均不计,从静止开始放手让它们运动,取g=10m/s2。求:
(1)、物体A着地时的速度?
(2)、物体B沿斜面上滑的最大距离?
如图所示,滑动变阻器的总电阻R=60Ω,A、B间的电压U=18V且保持不变,R0=60Ω,先将开关S断开,移动滑片P使电压表示数为9.0V,然后将开关S闭合,若忽略电表对电路的影响,则电压表、电流表的示数分别为多少?
一台电风扇额定功率为44W,线圈电阻是5Ω,接于220V电压下正常工作。电风扇正常工作时,它输出的机械功率是多少?
接通电源后,电风扇因为故障不能转动,这时它的发热功率为多大?
如图所示,在竖直方向上A、B两物体通过劲度系数为k的轻质弹簧相连,A放在水平地面上;B、C两物体通过细绳绕过轻质定滑轮相连,C放在固定的光滑斜面上.用手拿住C,使细线刚刚拉直但无拉力作用,并保证ab段的细线竖直、cd段的细线与斜面平行.已知A、B的质量均为m,C的质量为4m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放C后它沿斜面下滑,A刚离开地面时,B获得最大速度,求: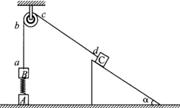
斜面倾角α.
B的最大速度VBm.
水平桌面上有带一圆弧形凸起的长方形木块A,木块A上的物体B用绕过凸起的轻绳与物体C相连,B与凸起之间的绳是水平的.用一水平向左的拉力作用在物体B上,恰好使物体A、B、C保持相对静止,如图所示。已知物体A、B、C的质量均为m,重力加速度为g,不计所有的摩擦,问拉力F应为多大?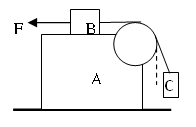
有带电平行板电容器竖直安放如图所示,两板间距d="0.1" m,电势差U="1000" V,现从平行板上A处以vA="3" m/s速度水平向左射入一带正电小球(知小球带电荷量q=10-7 C,质量m="0.02" g),经一段时间后发现小球打在A点正下方的B处,求:在图上粗略画出带电小球从A运动到B的轨迹。
算出A、B间的距离sAB;
小球到达B点时的动能.(g取10 m/s2)