如图所示为一物体沿直线运动的x﹣t图象,根据图象,求: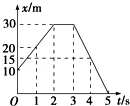
(1)第2s内的位移,第4s内的位移,前5s的总路程和位移
(2)各段的速度
(3)画出对应的v﹣t图象.
如图所示,匀强磁场的磁感强度B=0.20T,方向沿x轴正方向,且ab=40cm,bc=30cm,ac=50cm,且abc所在平面与xOz平面平行,分别求出通过面积abod、bofc、acfd的磁通量 、
、 、
、

在如图所示的空间区域里,y轴左方有一匀强电场,场强方向跟y轴负方向成30°角,大小为E = 4.0×105N/C,y轴右方有一垂直纸面的匀强磁场,有一质子以速度υ0 = 2.0×106m/s由x轴上A点(OA =" 10" cm)先后两次进入磁场,第一次沿x轴正方向射入磁场,第二次沿x轴负方向射入磁场,回旋后都垂直射入电场,最后又进入磁场,已知质子质量m为1.6×10-27kg,不计质子重力,求: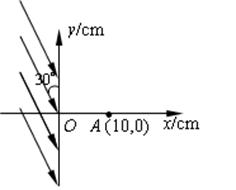
(1)匀强磁场的磁感应强度大小和方向;
(2)质子两次在磁场中运动的时间之比;
(3)质子两次在电场中运动的时间各为多少?
如图所示,有一质子经电压U0加速后,进入两块间距为d电压为U的平行金属板间,若质子从两板正中间垂直电场方向射入,且正好能穿出电场,求:
(1)金属板的长L;
(2)质子穿出电场时的动能;
(3)若题中质子改为α粒子,则(1)(2)中的问题结果是否改变?
有一金属细棒ab,质量m=0.05kg,电阻不计,可在两条轨道上滑动,如图所示,轨道间距为L=0.5m,其平面与水平面的夹角为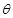 =37°,置于垂直于轨道平面向上的匀强磁场中,磁感应强度为B=1.0T,金属棒与轨道的动摩擦因数μ=0.5,(设最大静摩擦力与滑动摩擦力大小相等)回路中电源电动势为E=3V,内阻r=0.5Ω。 (g=10m/s2,sin37°=0.6,cos37°=0.8)求:
=37°,置于垂直于轨道平面向上的匀强磁场中,磁感应强度为B=1.0T,金属棒与轨道的动摩擦因数μ=0.5,(设最大静摩擦力与滑动摩擦力大小相等)回路中电源电动势为E=3V,内阻r=0.5Ω。 (g=10m/s2,sin37°=0.6,cos37°=0.8)求:
(1)为保证金属细棒不会沿斜面向上滑动,流过金属细棒ab的电流的最大值为多少?
(2)滑动变阻器R的阻值应调节在什么范围内,金属棒能静止在轨道上?
如图所示,足够大的荧光屏ON垂直xOy坐标面,与x轴夹角为30°,当y轴与ON间有沿+y方向、场强为E的匀强电场时,一质量为m、电荷量为-q的离子从y轴上的P点,以速度v0、沿+x轴方向射入电场,恰好垂直打到荧光屏上的M点(图中未标出).现撤去电场,在y轴与ON间加上垂直坐标面向里的匀强磁场,相同的离子仍以速度v0从y轴上的Q点沿+x轴方向射入磁场,恰好也垂直打到荧光屏上的M点,离子的重力不计.求: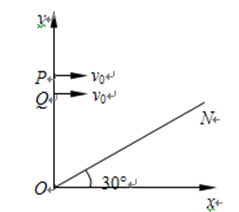
(1)离子在电场中运动的时间t1;
(2)P点距O点的距离y1和离子在磁场中运动的加速度大小a;
(3)若相同的离子分别从y轴上的不同位置以速度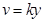 (
(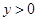 ,k为常数)、沿+x轴方向射入磁场,离子都能打到荧光屏上,k应满足的条件.
,k为常数)、沿+x轴方向射入磁场,离子都能打到荧光屏上,k应满足的条件.