为了解某地区观众对某大型综艺节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众观看该节目的场数与所对应的人数的表格:
将收看该节目场数不低于13场的观众称为“歌迷”,已知“歌迷”中有10名女性.
根据已知条件完成下图的 列联表,并判断我们能否有95%的把握认为“歌迷”与性别有关?
列联表,并判断我们能否有95%的把握认为“歌迷”与性别有关?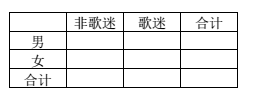
将收看该节目所有场数(14场)的观众称为“超级歌迷”,已知“超级歌迷”中有2名女性,若从“超级歌迷”中任意选取2人,求至少有1名女性观众的概率.
注: ,
,
已知|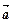 |=,|
|=,|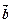 |=2.
|=2.
(1)若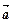 与
与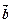 的夹角为150°,求|
的夹角为150°,求|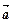 +2
+2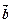 |;
|;
(2)若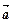 -
-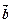 与
与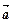 垂直,求
垂直,求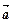 与
与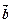 的夹角大小.
的夹角大小.
在△ABC中,角A、B、C所对应的边分别为a,b,c,已知a=3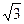 ,c=2,B=150°,求边b的长及A的正弦值.
,c=2,B=150°,求边b的长及A的正弦值.
(本小题10分)
对于函数f(x)(x )恒有f(ab)=f(a)+f(b)且x>1时f(x)>0 ,f(2)=1
)恒有f(ab)=f(a)+f(b)且x>1时f(x)>0 ,f(2)=1
(1)求f(4)、f(1)、f(-1)的值;
(2)求证f(x)为偶函数;
(3)求证f(x)在(0,+ )上是增函数;
)上是增函数;
(4)解不等式f(x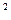 -5)<2.
-5)<2.
(本小题10分)
已知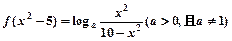 。
。
(1)求f(x)的解析式,并写出定义域;
(2)判断f(x)的奇偶性并证明;
(3)当a>1时,求使f(x) 成立的x的集合。
成立的x的集合。
(本小题10分)
已知函数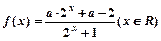 是奇函数
是奇函数
(1)求实数 a的值;(2)判断并证明函数f(x)的单调性。
a的值;(2)判断并证明函数f(x)的单调性。