在平面直角坐标系中,以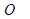 为极点,
为极点, 轴非负半轴为极轴建立极坐标系,已知曲线
轴非负半轴为极轴建立极坐标系,已知曲线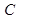 的极坐标方程为
的极坐标方程为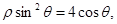 直线
直线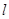 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线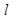 与曲线
与曲线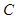 交于
交于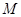 ,
,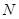 两点.
两点.
(1)写出曲线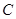 的直角坐标方程和直线
的直角坐标方程和直线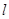 的普通方程
的普通方程
(2)若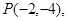 求
求 的值
的值
选修4-4:坐标系与参数方程
已知直线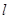 的参数方程为
的参数方程为 (t为参数),若以平面直角坐标系
(t为参数),若以平面直角坐标系 的O点为极点,
的O点为极点, 轴正半轴为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为
轴正半轴为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为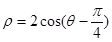 。
。
(1)求直线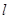 的倾斜角;
的倾斜角;
(2)若直线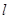 与曲线C交于不同的两点A,B,求AB的长。
与曲线C交于不同的两点A,B,求AB的长。
选修4-1:几何证明选讲
如图,⊙O是以AB为直径的△ABC的外接圆,点D是劣弧 的中点,连结AD并延长与过点C的切线交于点P,OD与BC相交于点E。
的中点,连结AD并延长与过点C的切线交于点P,OD与BC相交于点E。
(1)求证: ;
;
(2)求证: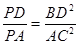

已知函数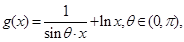 在
在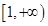 上为增函数,
上为增函数, 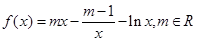
(1)求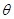 的值; (2)若
的值; (2)若 在
在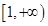 上为单调函数,求
上为单调函数,求 的取值范围;
的取值范围;
(3)设 ,若在
,若在 上至少存在一个
上至少存在一个 ,使得
,使得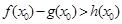 成立,求
成立,求 的范围。
的范围。
如图,设抛物线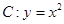 的焦点为
的焦点为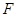 ,动点
,动点 在直线
在直线 上
上
运动,过P作抛物线C的两条切线PA,PB,且与抛物线C分别相切于A,B两点.
(1)求△APB的重心G的轨迹方程.
(2)证明∠PFA=∠PFB.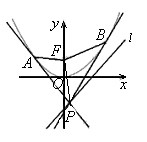
已知正方形ABCD的边长为2, ,
,
将正方形ABCD沿对角线BD折起,使 ,得到三棱锥
,得到三棱锥 ,如图所示。
,如图所示。
(1)当a=2时,求证: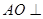 平面BCD;
平面BCD;
(2)当二面角 的大小为
的大小为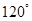 时,
时,
求二面角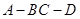 的正切值。
的正切值。