如图所示是倾角θ=37º的固定光滑斜面,两端有垂直于斜面的固定挡板P、Q,PQ距离L=2m,质量M=1.0kg的木块A(可看成质点)放在质量m="0.5kg" 的长d=0.8m的木板B上并一起停靠在挡板P处,A木块与斜面顶端的电动机间用平行于斜面不可伸长的轻绳相连接,现给木块A沿斜面向上的初速度,同时开动电动机保证木块A一直以初速度v0=1.6m/s沿斜面向上做匀速直线运动,已知木块A的下表面与木板B间动摩擦因数μ1=0.5,经过时间t,当B板右端到达Q处时刻,立刻关闭电动机,同时锁定A、B物体此时的位置。然后将A物体上下面翻转,使得A原来的上表面与木板B接触,已知翻转后的A、B接触面间的动摩擦因数变为μ2=0.25,且连接A与电动机的绳子仍与斜面平行。现在给A向下的初速度v1=2m/s,同时释放木板B,并开动电动机保证A木块一直以v1沿斜面向下做匀速直线运动,直到木板B与挡板P接触时关闭电动机并锁定A、B位置。求:

(1)B木板沿斜面向上加速运动过程的加速度大小;
(2)A、B沿斜面上升过程所经历的时间t;
(3)A、B沿斜面向下开始运动到木板B左端与P接触 时,这段过程中A、B间摩擦产生的热量。
一辆小汽车通过长1100米的隧道,小汽车刚进隧道时的速度是10m/s,出隧道时的速度是12m/s,(小汽车可看成质点)求:小汽车过隧道时的加速度是多大?
通过隧道所用的时间是多少?
如图所示,一木块质量为m,放在倾角为θ的静止斜面上,木块间的动摩擦因数为μ,当用一水平方向的力F推这木块时,木块沿斜面匀速上升,请画出受力分析图并求这水平作用力F的大小。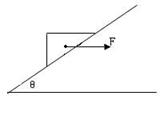
如图,物体A与B用跨过滑轮的细绳相连,已知物体B的重力为80N,地面对B的支持力为60N,连接物体B的细绳与水平地面夹角为30°,所有物体保持静止。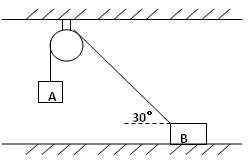
计算物体A的重力
计算地面对物体B的摩擦力
若物体B在水平向右外力作用下匀速向右运动过程中,请判断水平外力及地面对物体B摩擦力的变化情况。(设物体A未升至滑轮处)
跳伞运动员做低空跳伞表演,他离开飞机后先做自由落体运动,当距离地面 125 m时打开降落伞,伞张开后运动员就以14.3 m/s2的加速度做匀减速运动,到达地面时速度为5 m/s,问:运动员离开飞机时距地面的高度为多少?
离开飞机后,经过多长时间才能到达地面?(g="10" m/s2)
如图所示,一名骑独轮车的杂技演员在空中钢索上表演,如果演员与独轮车的总质量为80 kg,两侧的 钢索互成150°夹角,求钢索所受拉力有多大?(钢索自重不计,取cos 75°= 0.26, g="10" m/s2)