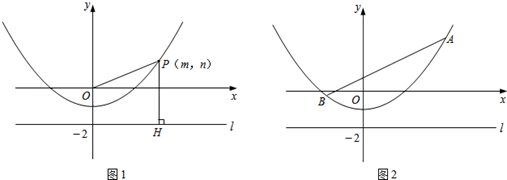
如图1，P（m，n）是抛物线y=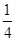
x2-1上任意一点，l是过点（0，﹣2）且与x轴平行的直线，过点P作直线PH⊥l，垂足为H．
（1）填空：当m=0时，OP= ，PH= ；当m=4时，OP= ，PH= ．
（2）对任意m，n，猜想OP与PH的大小关系，并证明你的猜想．
（3）连接OH，是否存在这样的点P，使得△OPH为等边三角形？如果存在，求出点P的坐标；如果不存在，请说明理由．
（4）如图2，已知线段AB=6，端点A，B在抛物线y=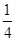x2-1上滑动，求A，B两点到直线l的距离之和的最小值．
解下列方程：
（1）3（x﹣2）=x﹣（7﹣8x）；
（2）
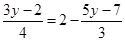
某鞋店销售一种新款女鞋，10天内共售出这种款式的女鞋46双，下面是售货员按卖出的顺序记录的上述46双鞋的鞋号：
23．5，23．5，23，23．5，24，23．5，22，24．5，
23．5，23．5，25，24，23．5，23，23，24．5，
23，23．5，23．5，22．5，22．5，23．5，23．5，23．5，
23．5，24，23，22．5，24，23．5，23．5，25，
22，22．5，24，22．5，23，24，23，23，
24，23，23，24，22，24．5
（1）你能设法将上述数据整理得较为清楚吗？
（2）请画出各种鞋号销售情况的条形统计图；
（3）鞋号为23．5和24的女鞋共销售了多少双？占这种女鞋销售量的百分比是多少？
（4）请你对鞋店的进货提出一条合理化建议．
计算：
．
计算：
．
如图，已知AB是⊙O的弦，CD是⊙O的直径，CD⊥AB，垂足为E，且点E是OD的中点，⊙O的切线BM与AO的延长线相交于点M，连接AC，CM．
（1）若AB=
，求
的长；（结果保留π）
（2）求证：四边形ABMC是菱形．