已知:y关于x的函数 的图象与x轴有交点.
的图象与x轴有交点.
(1)求k的取值范围;
(2)若 ,
, 是函数图象与x轴两个交点的横坐标,且满足
是函数图象与x轴两个交点的横坐标,且满足 .
.
①求k的值;
②当k≤x≤k+2时,请结合函数图象确定y的最大值和最小值.
先化简,再求值: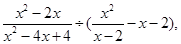 其中
其中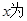 不等式组
不等式组 的整数解.
的整数解.
解方程: +
+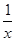 =1
=1
计算:计算: -(
-(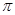 -
- )0+
)0+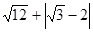 —
—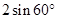
(本题满分10分)
如图,在平面直角坐标系中,直线AB: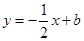 分别与x轴、y轴交于点A、B,
分别与x轴、y轴交于点A、B, .
.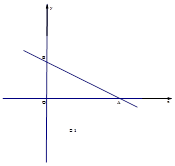
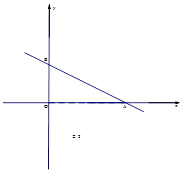
(1)求b的值.
(2)动点C从A点出发以2个单位/秒的速度沿x轴的正半轴运动,动点D从B点出发以1个单位/秒的速度沿y轴的正半轴运动.运动时间为t(t>0),过A作x轴的垂线交直线CD于点P,过P作y轴的垂线交直线AB于点F,设线段BF的长为d(d>0),求d与t的函数关系式.
(3)在(2)的条件下,以点A为圆心,2为半径作⊙A,过点C作不经过第三象限的直线l与⊙A相切,切点为Q, 直线l与y轴交于点E,作QH⊥AE于H,交x轴于点G,是否存在t值,使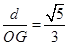 ,若存在,求出t值;若不存在,请说明理由.
,若存在,求出t值;若不存在,请说明理由.
(本题满分8分)
为响应市政府“创建国家森林城市”的号召,某小区计划购进A、B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元.
(1)若购进A、B两种树苗刚好用去1220元,问购进A、B两种树苗各多少棵?
(2)若购买的A种树苗的数量大于B种树苗的数量,请你给出一种费用最省的方案.