如图,⊙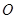 的半径为6,线段
的半径为6,线段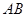 与⊙
与⊙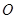 相交于点
相交于点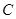 、
、 ,
, ,
, ,
,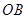 与⊙
与⊙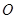 相交于点
相交于点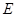 .
.
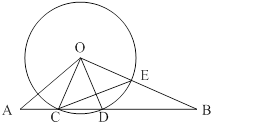
(1)求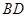 长;
长;
(2)当 ⊥
⊥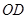 时,求证:
时,求证: .
.
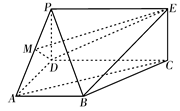
如图,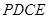 为矩形,
为矩形,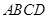 为梯形,平面
为梯形,平面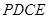
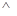 平面
平面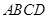 ,
,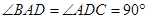 ,
,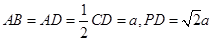 .
.
(Ⅰ)若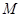 为
为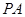 中点,求证:
中点,求证: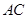 ∥平面
∥平面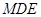 ;
;
(Ⅱ)求平面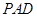 与
与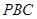 所成锐二面角的大小.
所成锐二面角的大小.
两个人在进行一项掷骰子放球游戏中,规定:若掷出1点,甲盒中放一球;
若掷出2点或3点,乙盒中放一球;若掷出4点或5点或6点,丙盒中放一球,前后共掷3次,设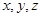 分别表示甲,乙,丙3个盒中的球数.
分别表示甲,乙,丙3个盒中的球数.
(Ⅰ)求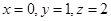 的概率;
的概率;
(Ⅱ)记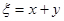 ,求随机变量
,求随机变量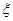 的概率分布列和数学期望.
的概率分布列和数学期望.
在平面直角坐标系 中,设锐角
中,设锐角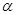 的始边与
的始边与 轴的非负半轴重合,终边与单位圆交于点
轴的非负半轴重合,终边与单位圆交于点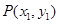 ,将射线
,将射线 绕坐标原点
绕坐标原点 按逆时针方向旋转
按逆时针方向旋转 后与单位圆交于点
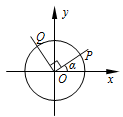
后与单位圆交于点 . 记
. 记 .
.
(Ⅰ)讨论函数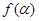 的单调性;
的单调性;
(Ⅱ)设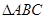 的角
的角 所对的边分别为
所对的边分别为 ,若
,若 ,且
,且 ,
,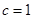 ,求
,求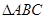 的面积.
的面积.
选修4-5:不等式选讲
已知函数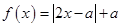 .
.
(Ⅰ)若不等式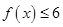 的解集为
的解集为 ,
, ,求证:
,求证: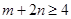 .
.
(Ⅱ)若在(Ⅰ)的条件下,存在实数t,使得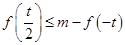 成立,求实数m的取值范围.
成立,求实数m的取值范围.
选修4-5:不等式选讲
已知函数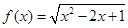 ,
,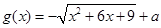
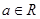
(Ⅰ)解关于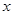 的不等式
的不等式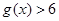
(Ⅱ)若函数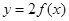 的图象恒在函数
的图象恒在函数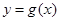 的上方,求实数
的上方,求实数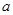 的取值范围.
的取值范围.