(本小题满分14分)
设直线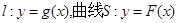 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R,都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R,都有 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.
(Ⅰ)已知函数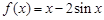 .求证:
.求证: 为曲线
为曲线 的“上夹线”.
的“上夹线”.
(Ⅱ)观察下图:
根据上图,试推测曲线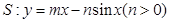 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.
已知 是椭圆
是椭圆 上的一点,求
上的一点,求 到
到 (
( )的距离的最小值.
)的距离的最小值.
若在边长为 的正三角形
的正三角形 的边
的边 上有
上有 (
( N*,
N*, )等分点,沿向量
)等分点,沿向量 的方向依次为
的方向依次为 ,记
,记 ,若给出四个数值:①
,若给出四个数值:① ②
② ③
③ ④
④ ,则
,则 的值不可能的共有()
的值不可能的共有()
| A.1个 | B.2个 | C.3个 | D.4个 |
已知数列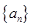 是等差数列,其前n项和为Sn,若
是等差数列,其前n项和为Sn,若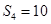 ,
,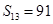 .
.
(1)求 ;
;
(2)若数列{Mn}满足条件: 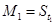 ,当
,当 时,
时,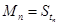 -
-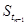 ,其中数列
,其中数列 单调递增,且
单调递增,且 ,
, .
.
①试找出一组 ,
,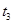 ,使得
,使得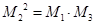 ;
;
②证明:对于数列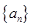 ,一定存在数列
,一定存在数列 ,使得数列
,使得数列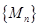 中的各数均为一个整数的平方.
中的各数均为一个整数的平方.
如图,在平面直角坐标系 中,已知椭圆
中,已知椭圆 :
: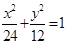 ,设
,设 是椭圆
是椭圆 上的任一点,从原点
上的任一点,从原点 向圆
向圆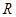 :
: 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点 ,
,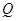 .
.
(1)若直线 ,
, 互相垂直,求圆
互相垂直,求圆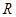 的方程;
的方程;
(2)若直线 ,
, 的斜率存在,并记为
的斜率存在,并记为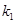 ,
,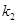 ,求证:
,求证: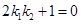 ;
;
(3)试问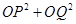 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
已知函数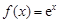 (其中
(其中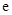 是自然对数的底数),
是自然对数的底数),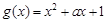 ,
,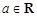 .
.
(1)记函数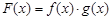 ,且
,且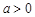 ,求
,求 的单调增区间;
的单调增区间;
(2)若对任意
 ,
, ,均有
,均有 成立,求实数
成立,求实数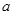 的取值范围.
的取值范围.