已知 是椭圆
是椭圆 上的一点,求
上的一点,求 到
到 (
( )的距离的最小值.
)的距离的最小值.
已知数列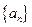 满足递推关系式:
满足递推关系式: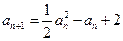 ,
,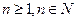 .
.
(1)若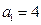 ,证明:(ⅰ)当
,证明:(ⅰ)当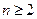 时,有
时,有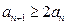 ;(ⅱ)当
;(ⅱ)当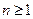 时,有
时,有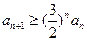 .
.
(2)若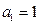 ,证明:当
,证明:当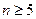 时,有
时,有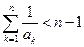 .
.
过点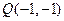 作已知直线
作已知直线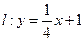 的平行线,交双曲线
的平行线,交双曲线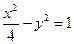 于点
于点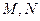 .
.
(1)证明:点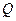 是线段
是线段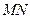 的中点.
的中点.
(2)分别过点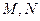 作双曲线的切线
作双曲线的切线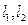 ,证明:三条直线
,证明:三条直线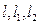 相交于同一点.
相交于同一点.
(3)设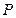 为直线
为直线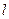 上一动点,过点
上一动点,过点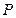 作双曲线的切线
作双曲线的切线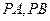 ,切点分别为
,切点分别为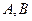 .证明:点
.证明:点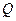 在直线AB上.
在直线AB上.
已知函数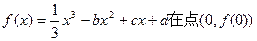 处的切线方程为
处的切线方程为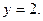
(I)求c、d的值;
(II)求函数f(x)的单调区间。
某校有5名学生报名参加义务献血清治疗重症甲流患者活动, 这5人中血型为A型的2名, 血型为B型的学生1 名,血型为O型的学生2名,已知这5名学生中每人符合献血条件的概率均为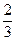
 (1)若从这5名学生中选出2名,求所选2人血型为O型或A型的概率
(1)若从这5名学生中选出2名,求所选2人血型为O型或A型的概率
(2)求这5名学生中至少有2名学生符合献血条件的概率.
如图所示,已知直四棱柱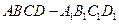 中,
中,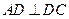 ,
,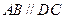 ,且满足
,且满足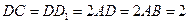
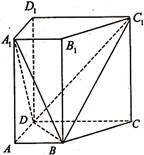
(I)求证: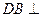 平面
平面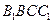 ;
;
(Ⅱ)求二面角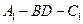 的余弦值。
的余弦值。