某市政府欲在如图所示的矩形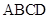 的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形
的非农业用地中规划出一个休闲娱乐公园(如图中阴影部分),形状为直角梯形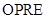 (线段
(线段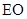 和
和 为两条底边),已知
为两条底边),已知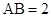
 ,
,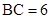
 ,
,
 ,其中曲线
,其中曲线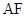 是以
是以 为顶点、
为顶点、 为对称轴的抛物线的一部分.
为对称轴的抛物线的一部分.
(1)求曲线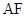 与
与 ,
,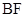 所围成区域的面积;
所围成区域的面积;
(2)求该公园的最大面积.
(本小题满分12分)已知等差数列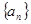 中,
中, ,
,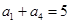 ,
,
(1)求数列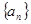 的通项公式;
的通项公式;
(2)若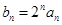 ,求数列
,求数列 的前
的前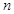 项和
项和 .
.
(本小题满分12分)在△ 中,角
中,角 ,
,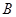 ,
,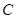 ,的对边分别为
,的对边分别为 .已知向量
.已知向量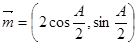 ,
,  ,
,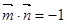 .
.
(1)求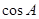 的值;
的值;
(2)若 ,求△
,求△ 周长的最大值.
周长的最大值.
(本小题满分12分)已知数列 的前
的前 项和为
项和为 ,
,
(1)若 ,求
,求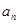 ;
;
(2)若 ,求
,求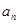 .
.
(本小题满分10分)如图,为了测量哈尔滨市第三中学教学楼的高度,某人站在 处测得楼顶
处测得楼顶 的仰角为
的仰角为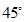 ,前进18
,前进18 后,到达
后,到达 处测得楼顶
处测得楼顶 的仰角为
的仰角为 ,试计算教学楼的高度.
,试计算教学楼的高度.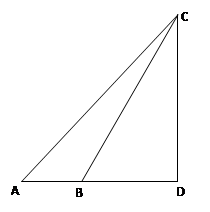
已知曲线 y = x3 + x-2 在点 P0 处的切线 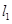 平行直线4x-y-1=0,且点 P0 在第三象限,
平行直线4x-y-1=0,且点 P0 在第三象限,
⑴求P0的坐标; ⑵若直线  , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.