某商场打出了促销广告如下表，对顾客实行优惠．
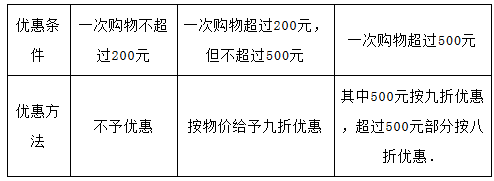
（1）某人在此商场两次购物分别付款168元和423元，则他第一次付款168元，可购标价总值是 元的货物；第二次付款423元，可购标价总值是 元的货物．请列式计算：若他把两次购得的货物合在一次买，需要付多少钱？
（2）如果字母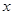
（x>200）表示某顾客在此商场一次购物的货物标价总值，那么所付款数该如何用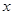的代数式表示呢？
（本题6分）某校图书馆上周借书记录（超过100册的部分记为正，少于100册的部分记为负）如下表：
| 星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
| ＋18 |
－6 |
＋15 |
0 |
－12 |
（1）上星期五借出多少册书？
（2）上星期借书最多的一天比借书最少的一天多借出图书多少册？
（3）上星期平均每天借出多少册书？
（本题8分）已知：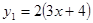
，
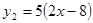，当x取何值时
（1）y1与y2互为相反数？
（2）y1比y2小2？
解方程（每题4分，共8分）
（1）
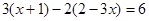（2）－
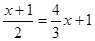
先化简，再求值（每题4分，共8分）
（1）
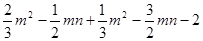，其中m=－1,n=2
（2）
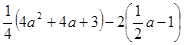，其中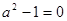
探索性问题：
已知：b是最小的正整数，且a、b满足（c-5）2+|a+b|=0，请回答问题：
（1）请直接写出a、b、c的值．a= ，b= ，c= ；
（2）数轴上a、b、c三个数所对应的点分别为A、B、C，点A、B、C同时开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动，假设t秒钟过后，若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC．
①t秒钟过后，AC的长度为 （用t的关系式表示）；
②请问：BC-AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．