设计一个商标图案(如图阴影部分),其中O为半圆的圆心,AB=a,BC=b,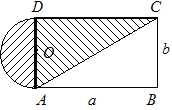
(1)用关于a,b的代数式表示商标图案的面积S;
(2)求当a=6cm,b=4cm时S的值.(本题结果都保留π)
某楼盘准备以每平方米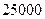 元的均价对外销售,由于国务院有关房地产的新政策出台,购房者持币观望.为了加快资金周转,房地产开发商对价格进行两次下调,最终以每平方米
元的均价对外销售,由于国务院有关房地产的新政策出台,购房者持币观望.为了加快资金周转,房地产开发商对价格进行两次下调,最终以每平方米 元的均价开盘销售.
元的均价开盘销售.求平均每次下调的百分率
某人准备以每平方米
 元的均价购买一套
元的均价购买一套 平方米的房子.开发商还给予以下两种优惠方案以供选择:①一次付清全款打九九折;②一次付清全款不打折,送五年物业管理费.如该楼盘物业管理费是每月
平方米的房子.开发商还给予以下两种优惠方案以供选择:①一次付清全款打九九折;②一次付清全款不打折,送五年物业管理费.如该楼盘物业管理费是每月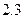 元/米2.请问哪种方案更优惠?
元/米2.请问哪种方案更优惠?
如图,在平面直角坐标系中,Rt△OAB的直角边OA在x轴的正半轴上,点B在第象限,将△OAB绕点O按逆时针方向旋转至△OA′B′,使点B的对应点B′落在y轴的正半轴上,已知OB=2,

求点B和点A′的坐标;
求经过点B和点B′的直线所对应的一次函数解析式,并判断点A是否在直线BB′上。
如图,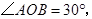 过
过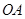 上到点
上到点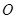 的距离为1,3,5,7,…的点作
的距离为1,3,5,7,…的点作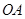 的垂线,分别与
的垂线,分别与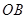 相交,得到图所示的阴影梯形,它们的面积依次记为
相交,得到图所示的阴影梯形,它们的面积依次记为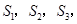 ….则
….则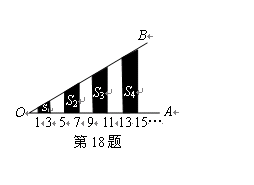
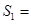 ;
;通过计算可得
 .
.
.上海股民杨百万上星期五交易结束时买进某公司股票1000股,每股50 元,下表为本周内每日该股的涨跌情况 (星期六、日股市休市) (单位:元)
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 每股涨跌 |
+4 |
+4.5 |
-1 |
2.5 |
-5 |
星期三收盘时,每股是多少元?
本周内每股最高价多少元?最低价是多少元?
已知买进股票还要付成交金额2‰ 的手续费,卖出时还需付成交额2‰ 的手续费和1‰交易税,如果在星期五收盘前将全部股票卖出,他的收益情况如何?
(注意:‰不是百分号,是千分号)
用3根火柴棒搭成1个三角形,接着用火柴棒按如图所示的方式搭成2个三角形,再用火柴棒搭成3个三角形、4个三角形……
(1)若这样的三角形有6个时,则需要火柴棒根.
(2)若这样的三角形有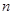 个时,则需要火柴棒根.
个时,则需要火柴棒根.
(3)若用了2001根火柴棒,则可组成这样图案的三角形有个.