已知数列 的通项
的通项 (
( ),我们把使
),我们把使 为整数的
为整数的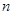 叫做优数,则在
叫做优数,则在 内所有优数的和为( )
内所有优数的和为( )
A.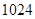 |
B. |
C. |
D.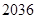 |
设z=1+i(i是虚数单位),则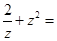 ()
()
A.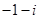 |
B.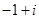 |
C. |
D.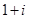 |
已知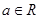 ,则“
,则“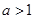 ”是“
”是“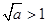 ”的()
”的()
| A.既不充分也不必要条件 | B.充要条件 |
| C.充分不必要条件 | D.必要不充分条件 |
已知 ,则
,则 ()
()
A. |
B. |
C. |
D. |
设函数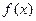 的定义域为D,若存在非零实数h使得对于任意
的定义域为D,若存在非零实数h使得对于任意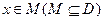 ,有
,有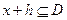 ,且
,且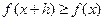 ,则称
,则称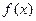 为M上的“h阶高调函数”。给出如下结论:
为M上的“h阶高调函数”。给出如下结论:
①若函数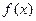 在R上单调递增,则存在非零实数h使
在R上单调递增,则存在非零实数h使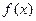 为R上的“
为R上的“ h阶高调函数”;
h阶高调函数”;
②若函数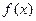 为R上的“h阶高调函数”,则
为R上的“h阶高调函数”,则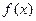 在R上单调递增;
在R上单调递增;
③若函数 为区间
为区间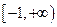 上的“h阶高诬蔑财函数”,则
上的“h阶高诬蔑财函数”,则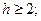
④若函数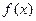 在R上的奇函数,且
在R上的奇函数,且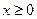 时,
时,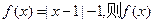 只能是R上的“4阶高调函数”。
只能是R上的“4阶高调函数”。
其中正确结论的序号为()
A.① ③ ③ |
B.①④ | C.②③ | D.②④ |
函数 的零点个数是()
的零点个数是()
| A.1 | B.2 | C.3 | D.4 |