某市“招手即停”公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算).
若某条线路的总里程为20公里,写出票价与里程之间的函数关系式,并求乘车16公里的票价.
(本小题满分12分)如图所示,直三棱柱 的各条棱长均为
的各条棱长均为 ,
, 是侧棱
是侧棱 的中点.
的中点.
(1)求证:平面 平面
平面 ;
;
(2)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(3)求平面 与平面
与平面 所成二面角(锐角)的大小.
所成二面角(锐角)的大小.
(本小题满分12分)数列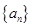 的前
的前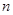 项和记为
项和记为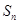 ,
,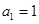 ,
,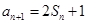 (
(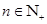 ).
).
(1)求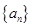 的通项公式;
的通项公式;
(2)等差数列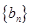 的各项为正,其前
的各项为正,其前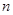 项和为
项和为 ,且
,且 ,又
,又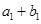 ,
, ,
, 成等比数列,求
成等比数列,求 .
.
(本小题满分12分)设函数 ,其中向量
,其中向量 ,
, .
.
(1)求函数 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在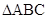 中,
中, 、
、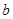 、
、 分别是角
分别是角 、
、 、
、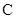 的对边,已知
的对边,已知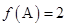 ,
, ,
,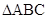 的面积为
的面积为 ,求
,求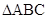 外接圆半径
外接圆半径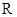 .
.
(本小题满分12分)设 是定义在
是定义在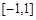 上的奇函数,函数
上的奇函数,函数 与
与 的图象关于
的图象关于 轴对称,且当
轴对称,且当 时,
时, .
.
(1)求函数 的解析式;
的解析式;
(2)若对于区间 上任意的
上任意的 ,都有
,都有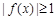 成立,求实数
成立,求实数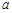 的取值范围.
的取值范围.
如图,O为坐标原点,点F为抛物线C1: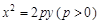 的焦点,且抛物线C1上点P处的切线与圆C2:
的焦点,且抛物线C1上点P处的切线与圆C2: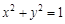 相切于点Q.
相切于点Q.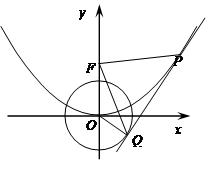
(Ⅰ)当直线PQ的方程为 时,求抛物线C1的方程;
时,求抛物线C1的方程;
(Ⅱ)当正数 变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求
变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求 的最小值.
的最小值.