某工厂为了检查一条流水线的生产情况，从该流水线上随机抽取40件产品，测量这些产品的重量（单位：克），整理后得到如下的频率分布直方图（其中重量的分组区间分别为（490，495]，（495，500]，（500，505]，（505，510]，（510，515]）
（1）若从这40件产品中任取两件，设X为重量超过505克 的产品数量，求随机变量X的分布列；
（2）若将该群体分别近似看作总体分布，现从该流水线上任取5件产品，求恰有两件产品的重量超过505克的概率．
已知
，点
满足
，记点的轨迹为
.
（Ⅰ）求轨迹的方程；（Ⅱ）若直线
过点
且与轨迹交于、
两点. （i）设点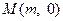
，问：是否存在实数
，使得直线绕点无论怎样转动，都有
成立？若存在，求出实数的值；若不存在，请说明理由.（ii）过、作直线
的垂线
、
，垂足分别为
、
，记
，求
的取值范围.
）袋中装着标有数字1，2，3的小球各2个，从袋中任取2个小球，每个小球被取出的可能性都相等．
（Ⅰ）求取出的2个小球上的数字互不相同的概率；
（Ⅱ）用
表示取出的2个小球上的数字之和，求随机变量的概率分布与数学期望．
设
是定义在[-1，1]上的偶函数，
的图象与的图象关于直线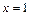
对称，
且当x∈[ 2，3 ] 时，
222233．（1）求的解析式；（2）若在
上为增函数，求
的取值范围；（3）是否存在正整数，使的图象的最高点落在直线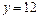
上？若存在，求出的值；若不存在，请说明理由．
如图所示，在直三棱柱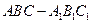
中，
，
，
，
，
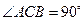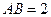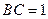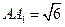是棱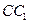
的中点．（Ⅰ）证明：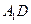
平面
；
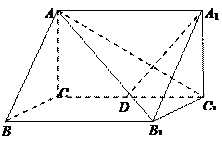
（Ⅱ）求二面角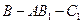
的余弦值．
已知向量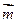
=(1，1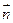)，向量
与向量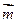的夹角为
,且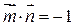
.
(1)求向量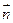； (2)设向量
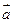=(1，0)，向量
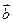=(cosx,2cos2(
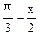)),其中0<x<
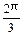，若
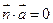,试求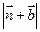
的取值范围.