设 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数, 的图象与
的图象与 的图象关于直线
的图象关于直线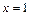 对称,
对称,
且当x∈[ 2,3 ] 时, 222233.(1)求
222233.(1)求 的解析式;(2)若
的解析式;(2)若 在
在 上为增函数,求
上为增函数,求 的取值范围;(3)是否存在正整数
的取值范围;(3)是否存在正整数 ,使
,使 的图象的最高点落在直线
的图象的最高点落在直线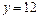 上?若存在,求出
上?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知直线 的参数方程为
的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (
(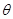 为参数).
为参数).
(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为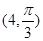 ,判断点P与直线
,判断点P与直线 的位置关系;
的位置关系;
(2)设点Q是曲线C上的一个动点,求点Q到直线 的距离的最小值与最大值.
的距离的最小值与最大值.
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连结EC、CD.
(Ⅰ)求证:直线AB是⊙O的切线;
(Ⅱ)若tan∠CED=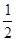 ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
已知函数 ,
, (
( ).
).
(1)求函数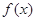 的单调区间;
的单调区间;
(2)求证:当 时,对于任意
时,对于任意 ,总有
,总有 成立.
成立.
“地沟油”严重危害了人民群众的身体健康,某企业在政府部门的支持下,进行技术攻关,新上了一种从“食品残渣”中提炼出生物柴油的项目,经测算,该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可以近似的表示为:
且每处理一吨“食品残渣”,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将补贴.
(1)当x∈[200,300]时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
已知直三棱柱ABC-A1B1C1中,AC=BC,点D是AB的中点. 
(1)求证:BC1∥平面CA1D;
(2)求证:平面CA1D⊥平面AA1B1B;
(3)若底面ABC为边长为2的正三角形,BB1=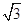 ,求三棱锥B1-A1DC的体积.
,求三棱锥B1-A1DC的体积.