(本小题满分12分)
如图,已知斜三棱柱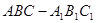 的侧面
的侧面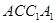 与底面ABC垂直,
与底面ABC垂直,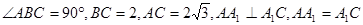
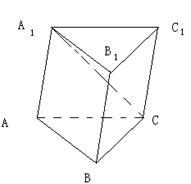
(1)求侧棱 与底面ABC所成的角;
与底面ABC所成的角;
(2)求侧面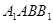 与底面ABC所成的角;
与底面ABC所成的角;
(3)求顶点C到平面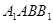 的距离.
的距离.
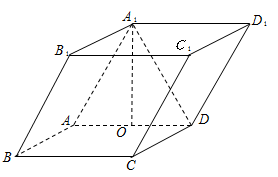
(本小题满分12分)如图,在四棱柱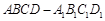 中,底面
中,底面 是矩形,且
是矩形,且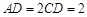 ,
, ,
,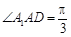 .若
.若 为
为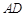 的中点,且
的中点,且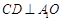 .
.
(1)求证: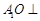 平面
平面 ;
;
(2)线段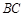 上是否存在一点
上是否存在一点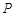 ,使得二面角
,使得二面角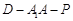 为
为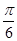 ?若存在,求出
?若存在,求出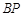 的长;不存在,说明理由.
的长;不存在,说明理由.
(本小题满分12分)
设数列 是公比小于1的正项等比数列,
是公比小于1的正项等比数列,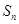 为数列
为数列 的前
的前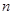 项和,已知
项和,已知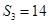 ,且
,且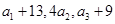 成等差数列。
成等差数列。
(1)求数列{an}的通项公式;
(2)若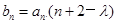 ,且数列
,且数列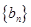 是单调递减数列,求实数
是单调递减数列,求实数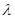 的取值范围。
的取值范围。
(本小题满分10分)已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8,高为4的等腰三角形,侧视图是一个底边长为6,高为4的等腰三角形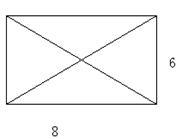
(1)求该几何体的体积V;
(2)求该几何体的侧面积S.
(本小题满分10分)
设
(1)求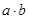 的最大值;
的最大值;
(2)求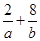 最小值.
最小值.