已知函数 ,(
,( 且
且 )恒过定点
)恒过定点 ,
,
(1)求实数 ;
;
(2)在(1)的条件下,将函数 的图象向下平移1个单位,再向左平移
的图象向下平移1个单位,再向左平移 个单位后得到函数
个单位后得到函数 ,设函数
,设函数 的反函数为
的反函数为 ,求
,求 的解析式;
的解析式;
(3)对于定义在 的函数
的函数 ,若在其定义域内,不等式
,若在其定义域内,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
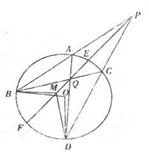
如图,过圆O外一点P作该圆的两条割线PAB和PCD,分别交圆 O于点A,B,C,D弦AD和BC交于Q点,割线PEF经过Q点交圆 O于点E、F,点M在EF上,且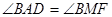 :
:
(I)求证:PA·PB=PM·PQ;(II)求证: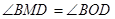 .
.
(本小题满分12分)
已知函数f(x)=ex+ax-1(e为自然对数的底数).
(Ⅰ)当a=1时,求过点(1,f(1))处的切线与坐标轴围成的三角形的面积;
(II)若f(x)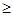 x2在(0,1 )上恒成立,求实数a的取值范围.
x2在(0,1 )上恒成立,求实数a的取值范围.
椭圆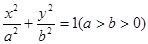 的左、右焦点分别为F1(-1,0),F2(1,0),过F1作与x轴不重合的直线l交椭圆于A,B两点.
的左、右焦点分别为F1(-1,0),F2(1,0),过F1作与x轴不重合的直线l交椭圆于A,B两点.
(Ⅰ)若ΔABF2为正三角形,求椭圆的离心率;
(Ⅱ)若椭圆的离心率满足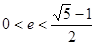 ,0为坐标原点,求证
,0为坐标原点,求证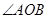 为钝角.
为钝角.
为了调查某大学学生在周日上网的时间,随机对1OO名男生和100名女生进行了不记 名的问卷调查.得到了如下的统计结果:
表1:男生上网时间与频数分布表
表2:女生上网时间与频数分布表
(I)若该大学共有女生750人,试估计其中上网时间不少于60分钟的人数;
(II)完成下面的2x2列联表,并回答能否有90%的把握认为“学生周日上网时间与性 别有关”?
表3: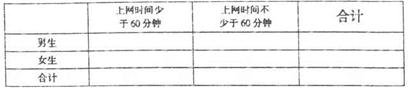

如图,在四棱锥P-ABCD中,PA丄平面ABCD,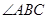 =
=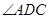 =90°
=90°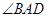 =1200,AD=AB=1,AC交BD于 O 点.
=1200,AD=AB=1,AC交BD于 O 点.
(I)求证:平面PBD丄平面PAC;
(Ⅱ)求三棱锥D-ABP和三棱锥B-PCD的体积之比.