设函数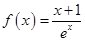 .
.
(1)求函数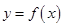 的最大值;
的最大值;
(2)对于任意的正整数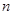 ,求证:
,求证: ;
;
(3)当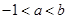 时,
时, 成立,求实数
成立,求实数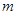 的最小值.
的最小值.
某食品厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费为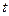 元(
元(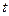 为常数,且
为常数,且 ,设该食品厂每公斤蘑菇的出厂价为
,设该食品厂每公斤蘑菇的出厂价为 元(
元( ),根据市场调查,销售量
),根据市场调查,销售量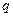 与
与 成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
(Ⅰ)求该工厂的每日利润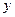 元与每公斤蘑菇
元与每公斤蘑菇 的出厂价
的出厂价 元的函数关系式;
元的函数关系式;
(Ⅱ)若 ,当每公斤蘑菇的出厂价
,当每公斤蘑菇的出厂价 为多少元时,该工厂的利润
为多少元时,该工厂的利润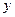 最大,并求最大值.
最大,并求最大值.
如图,在五面体ABCDEF中,FA
 平面ABCD,AD//BC//FE,AB
平面ABCD,AD//BC//FE,AB AD,AF=AB=BC=FE=
AD,AF=AB=BC=FE=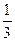 AD.
AD.
(Ⅰ)求异面直线BF与DE所成角的余弦值;
(Ⅱ)在线段CE上是否存在点M,使得直线AM与平面CDE所成角的正弦值为 ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.
已知数列 的前
的前 项和为
项和为 ,满足
,满足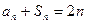 .
.
(Ⅰ)证明:数列 为等比数列,并求出
为等比数列,并求出 ;
;
(Ⅱ)设 ,求
,求 的最大项.
的最大项.
在锐角 中,
中, 三内角所对的边分别为
三内角所对的边分别为 .
.
设 ,
,
(Ⅰ)若 ,求
,求 的
的 面积;
面积;
(Ⅱ)求 的最大值.
的最大值.
在锐角 中,
中,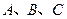 三内角所对的边分别为
三内角所对的边分别为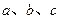 .
.
设 ,
,
(Ⅰ)若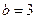 ,求
,求 的面积;
的面积;
(Ⅱ)求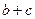 的最大值.
的最大值.