已知圆心为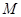 的圆方程为
的圆方程为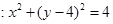 ,点
,点 是直线
是直线 上的一动点,过点
上的一动点,过点 作圆
作圆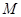 的切线
的切线 ,切点为
,切点为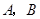 .
.
(1)当切线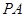 的长度为
的长度为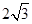 时,求点
时,求点 的坐标;
的坐标;
(2)若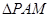 的外接圆为圆
的外接圆为圆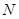 ,试问:当
,试问:当 在直线
在直线 上运动时,圆
上运动时,圆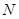 是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由.
是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由.
(3)求线段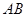 长度的最小值.
长度的最小值.
为了让学生了解更多“社会法律”知识,
| 分组 |
频数 |
频率 |
| 60.5~70.5 |
1 |
0.16 |
| 70.5~80.5 |
10 |
2 |
| 80.5~90.5 |
18 |
0.36 |
| 90.5~100.5 |
3 |
4 |
| 合计 |
50 |
1 |
某中学举行了一次“社会法律知识竞赛”,
共有800名学生参加了这次竞赛. 为了解
本次竞赛成绩情况,从中抽取了部分学
生的成绩(得分均为整数,满分为100
分)进行统计.请你根据尚未完成并有
局部污损的频率分布表,解答下列问题:
(1)若用系统抽样的方法抽取50个样本,
现将所有学生随机地编号为000,001,002,…,799,试写出第二组第一位学生的编号;
(2)填充频率分布表的空格1234并作出频率分布直方图;
(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约有多少人?
某商场设有会员卡,会员持卡消费都有一定的补贴,商场规定:购买物品不超过100元,补贴5%;购买物品超过100元而不超过5000元,补贴7%;购买物品超过5000元,补贴10%.画出输入消费 元时,输出商场补贴金额
元时,输出商场补贴金额 的程序框图.
的程序框图.
设计一个计算 值的一个流程图
值的一个流程图
某教师出了一份共3道题的测试卷,每道题1分。全班的3分、2分、1分和0分的学生所占的比例分别为30%,50%,10%和10%。
(1)若全班共10人,则平均分是多少?
(2)若全班共20人,则平均分是多少?
(3)若该班人数未知,能求出该班的平均分吗?
对于定义域为D的函数 ,若同时满足下列条件:①
,若同时满足下列条件:① 在D内单调
在D内单调
递增或单调递减;②存在区间[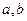 ]
] ,使
,使 在[
在[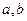 ]上的值域为[
]上的值域为[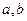 ];那么把
];那么把 (
( )叫闭函数。
)叫闭函数。
(1)求闭函数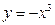 符合条件②的区间[
符合条件②的区间[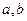 ];
];
(2)判断函数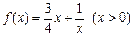 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若函数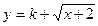 是闭函数,求实数
是闭函数,求实数 的取值范围。
的取值范围。