已知 是单调递增的等差数列,首项
是单调递增的等差数列,首项 ,前
,前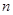 项和为
项和为 ;数列
;数列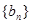 是等比数列,首项
是等比数列,首项
(1)求 的通项公式;
的通项公式;
(2)令 求
求 的前20项和
的前20项和 .
.
数列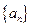 中
中 ,
,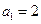 ,
, (
(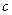 是不为零的常数,
是不为零的常数,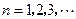 ),且
),且 成等比数列.
成等比数列.
(1)求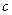 的值;
的值;
(2)求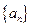 的通项公式;
的通项公式;
(3)求数列 的前
的前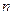 项之和
项之和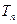
已知:函数
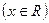
⑴ 求
求 的最小正周期;
的最小正周期;
⑵求 的单递增区间;
的单递增区间;
⑶求 图象的对称轴、对称中心。
图象的对称轴、对称中心。
如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB= ,BC=
,BC= 1,PA=2,E为PD的中点.
1,PA=2,E为PD的中点.
(1)求直线AC与PB所 成角的余弦值;
成角的余弦值;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出N点 到AB和AP的距离.
到AB和AP的距离.
已知向量 ,若正数k和t使得向量
,若正数k和t使得向量 垂直,求k的最小值.
垂直,求k的最小值.
已知点G是△ABC的重心,A(0, -1),B(0, 1),在x轴上有一点M,满足|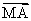 |=|
|=|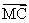 |,
|, (
(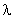 ∈R).
∈R).
⑴求点C的轨迹方程;
⑵若斜率为k的直线l与点C的轨迹交于不同两点P,Q,且满足|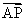 |=|
|=| |,试求k的取值范围.
|,试求k的取值范围.