某种产品的年产量不超过1000t,该产品的年产量(t)与费用(万元)之间的函数关系如图(1);该产品的年销售量(t)与每吨销售价(万元)之间的函数关系如图(2).
(1)设产品的费用为y(万元),试写出y与t的函数关系式.
(2)若生产出的产品都能在当年销售完,则年产量为多少吨时,当年可获得7500万元毛利润?(毛利润=销售额-费用)
已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.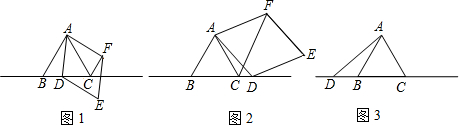
(1)如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.
如图,在平行四边形中,对角线AC⊥BC,AC=BC=2,动点P从点A出发沿AC向终点C移动,过点P分别作PM∥AB交BC于M,PN∥AD交DC于N.连结AM.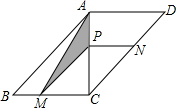
(1)四边形PMCN的形状有可能是菱形吗?请说明理由
(2)当AP=1时, 试求出四边形PMCN的面积。
如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长
如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3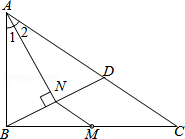
(1)求证:BN=DN;
(2)求△ABC的周长