如图所示,无限宽广的匀强磁场分布在xoy平面内,x轴上下方磁场均垂直xoy 平面向里,x轴上方的磁场的磁感应强度为B,x轴下方的磁场的磁感应强度为4B/3。现有一质量为m,电量为-q带负电粒子以速度v0从坐标原点O沿y方向进入上方磁场。在粒子运动过程中,与x轴交于若干点。不计粒子的重力。求:
(1)粒子在x轴上方磁场做匀速圆周运动半径r1
(2)如把x轴上方运动的半周与x轴下方运动的半周称为一周期的话,则每经过一周期,在x轴上粒子右移的平均速度。
(3)在与x轴的所有交点中,粒子两次通过同一点的坐标位置。
图为可测定比荷的某装置的简化示意图,在第一象限区域内有垂直于纸面向里的匀强磁场,磁感应强度大小B,在X轴上距坐标原点L的P处为离子的入射口,在Y上安放接收器,现将一带正电荷的粒子以v的速率从P处射入磁场,若粒子在y轴上距坐标原点L的M处被观测到,且运动轨迹半径恰好最小,设带电粒子的质量为m,电量为q,不计其重力。
(1)求上述粒子的比荷 ;
;
(2)如果在上述粒子运动过程中的某个时刻,在第一象限内再加一个匀强电场,就可以使其沿y轴正方向做匀速直线运动,求该匀强电场的场强大小和方向;
(3)为了在M处观测到按题设条件运动的上述粒子,在第一象限内的磁场可以局限在一个矩形区域内,求此矩形磁场区域的最小面积。
如图所示,将物体A放在容器B中,以某一速度把容器B竖直上抛,不计空气阻力,运动过程中容器B的地面始终保持水平, 证明:不论容器B上升还是下降,物体A对B的压力都等于零。
如图所示,正方形ABCD处在一个匀强电场中,电场线与正方形所在平面平行。已知A、B、C三点的电势依次为UA=6.0V,UB=4.0V,UC=-2.0V.(1)求D点的电势UD.(2)在图中画出过A点的电场线(要把作图过程画在图上,只画最后结果不能得分)。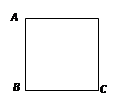
一辆摩托车行驶的最大速度为30m/s。现让该摩托车从静止出发,要在4分钟内追上它前方相距1千米、正以25m/s的速度在平直公路上行驶的汽车,则该摩托车行驶时,至少应具有多大的加速度?
如图所示,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,然后小球从轨道口B处飞出,最后落在水平面上,已知小球落地点C距B处的水平距离为3R.求小球对轨道口B处的压力为多大?